中文分词方法总结

本文介绍的是基于字符串匹配的中文分词的方法。
通过按照一定策略将待分析的汉字串与一个“词典”中的词条进行匹配,若在词典中找到某个字符串,则匹配成功。
字符串匹配算法:
在通过确定了词典后,目标句子可能含有很多词典中的词语。它们可能互相重叠,到底输出哪一个由规则决定。让我们来制定一些规则查词典。常用的规则有正向最长匹配、逆向最长匹配和双向最长匹配,它们都基于完全切分过程。
完全切分:
完全切分的思想是通过在句子中寻找出现在词典的单词。通过遍历句子中的字,查询该序列是否在字典中即可。
实现:
def fullSegment(text,dict):
res=[]
for i in range(len(text)):
for j in range(i+1,len(text)+1):
if(text[i:j] in dict):
res.append(text[i:j])
return res
结果如下:
print(fullSegment("南京市长江大桥",['南京','南京市','长江','大桥','长江大桥']))
['南京', '南京市', '长江', '长江大桥', '大桥']
正向最大匹配分词:
完全切分算法输出的并不是分词结果,为了输出真正的分词结果,需要完善规则,考虑到越长的单词表达的意义越丰富,于是我们定义单词越长优先级越高。具体说来,就是在以某个下标为起点递增查词的过程中,优先输出更长的单词,这种规则被称为最长匹配算法。该下标的扫描顺序如果从前往后,则为正向最大匹配。
算法思想:
-
从左向右取待切分汉语句的m个字符作为匹配字段,m为大机器词典中最长词条个数。
-
查找词典并进行匹配。若匹配成功,则将这个匹配字段作为一个词切分出来。
-
若匹配不成功,则将这个匹配字段的最后一个字去掉,剩下的字符串作为新的匹配字段,进行再次匹配,重复以上过程,直到切分出所有词为止。
实现:
def forwardSegment(text,dict):
res = []
i=0
while i < len(text):
long = text[i]
for j in range(i + 1, len(text) + 1):
long=text[i:j] if text[i:j] in dict and len(text[i:j])>len(long) else long
res.append(long)
i+=len(long)
return res
结果如下:
print(forwardSegment("南京市长江大桥",['南京','南京市','长江','大桥','长江大桥']))
['南京市', '长江大桥']
逆向最大匹配分词:
逆向匹配思想和正向是相同的,不过扫描顺序变成了从后至前。
实现:
def backSegment(text,dict):
res = []
i = len(text)-1
while i >= 0:
long = text[i]
for j in range(0, i):
long = text[j:i+1] if text[j:i+1] in dict and len(text[j:i+1]) > len(long) else long
res.insert(0,long)
i -= len(long)
return res
结果如下:
print(backSegment("南京市长江大桥",['南京','南京市','长江','大桥','长江大桥']))
['南京市', '长江大桥']
双向最大匹配分词:
有些句子用正向匹配能正确切分,而有些句子只能通过逆向匹配才能正确切分。

那么,具体该怎么使用匹配算法呢?我们一般通过如下规则来进行确定:
-
同时执行正向和逆向最长匹配,若两者的词数不同,则返回词数更少的那一个。
-
否则,返回两者中单字更少的那一个。当单字数也相同时,优先返回逆向最长匹配的结果。
实现:
def bidrectionalSegment(text,dict):
f=forwardSegment(text,dict)
b=backSegment(text,dict)
print(f)
print(b)
if(len(f)<len(b)):
return f
elif(len(f)>len(b)):
return b
else:
lenF=0
lenB=0
for i in b:
if len(i)==1:
lenB+=1
for j in f:
if len(j)==1:
lenF+=1
return f if lenF<lenB else b
结果如下:
print(bidrectionalSegment("研究生命起源",['研究','研究生','生命','起源']))
['研究生', '命', '起源'] #forward
['研究', '生命', '起源'] #back
['研究', '生命', '起源'] #bidrectional
总结:
字符串匹配方法算法简单,易于理解和实现,并且切分速度较快,成为分词方法中最流行的。因为字典匹配的方法不考虑具体的语言环境和定义,最大的缺点就是不能处理多词冲突和新词情况,严重依赖于词表,准确度较低。单纯采用字符串匹配的方法不能满足中文信息处理对分词结果准确度的要求。
提高词典匹配速度:
匹配算法的瓶颈之一在于如何判断集合词典中是否含有字符串。如果用有序集合,复杂度是O(logn)( n是词典大小);如果用散列表,时间复杂度虽然下降了,但内存复杂度却上去了。我们需要寻找一种速度又快、内存又省的数据结构。
字典树:
字典树(trie树)是一种特殊的前缀树结构。它是哈希树的一种变种,专门为字符串处理设计的数据结构。典型的应用是用于统计和排序大量的字符串(不限于字符串)因此经常被搜索引擎用于文字词频统计。优点:最大限度地减少无谓的字符串比较。Trie的核心思想是空间换时间,利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的
如图为一颗字典树,红色表示结束字符串,表示一个字符串的终止。
前缀树有三个基本性质:
-
根节点不包含字符,除根节点外每一个节点只包含一个字符。
-
从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
-
每个节点的所有子节点包含的字符都不相同。
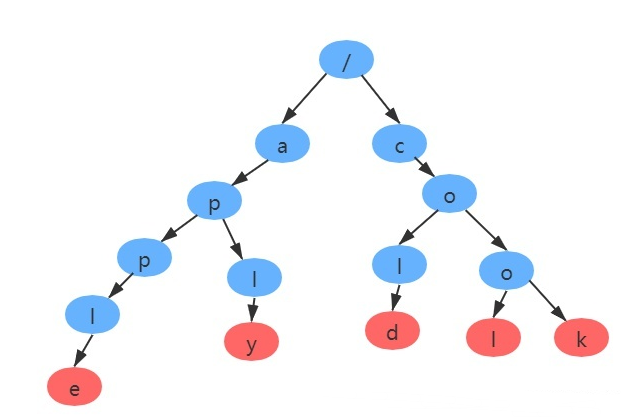
当我们需要查找apple ,字典树的查找步骤:/->a->p->p->l->e,此时e为结尾,说明apple存在字典树中。
当我们需要查找app,字典树的查找步骤:/->a->p->p,此时p不为字符串结尾,则app不存在字典树中。
实现:
class tree():
def __init__(self):
self.child={}
self.is_end=False
class Trie():
def __init__(self):
self.root=tree()
def insert(self,word)->None:
node=self.root
for char in word:
if char not in node.child:
node.child[char]=tree()
node=node.child[char]
node.is_end=True
def search(self,word):
node=self.root
for char in word:
if char not in node.child:
return False
node=node.child[char]
return node.is_end
trie=Trie()
for word in ['apple','app','aww']:
trie.insert(word)
print(trie.search("apple"))
print(trie.search("appl"))
True #trie.search("apple")
False#trie.search("appl")
当我们需要实现中英转换的时候,就需要对字典树加上映射。需要知道自己对应的值。我们约定用值为None表示节点不对应词语,虽然这样就不能插入值为None的键了,但实现起来更简洁。
class Node(object):
def __init__(self, value) -> None:
self._children = {}
self._value = value
def _add_child(self, char, value, overwrite=False):
child = self._children.get(char)
if child is None:
child = Node(value)
self._children[char] = child
elif overwrite:
child._value = value
return child
class Trie(Node):
def __init__(self) -> None:
super().__init__(None)
def __contains__(self, key): #函数可以在类的实例化对象上进行 in 操作.
return self[key] is not None
def __getitem__(self, key):#按下标访问数列的任意一项
state = self
for char in key:
state = state._children.get(char)
if state is None:
return None
return state._value
def __setitem__(self, key, value):#以与键相关联的方式存储值
state = self
for i, char in enumerate(key):
if i < len(key) - 1:
state = state._add_child(char, None, False)
else:
state = state._add_child(char, value, True)
Trie=Trie()
Trie["自然"]="nature"
print(Trie["自然"])
nature #output
AC自动机:
学习AC自动机必须掌握Trie树和KMP算法
AC自动机概述:
AC自动机是最一种多模式匹配算法,它由贝尔实验室的两位研究人员Alfred V. Aho 和 Margaret J.Corasick 于1975年发明,几乎与KMP算法同时问世,至今仍然在模式匹配领域被广泛应用。例如:在一篇文章中,需要找到多个词汇所在的位置和出现频率。
上节已经介绍了字典树,接下来介绍KMP算法,再进行融合介绍AC自动机。
KMP算法:
"字符串A是否为字符串B的子串?如果是的话出现在B的哪些位置?"该问题就是字符串匹配问题,字符串A称为模式串,字符串B称为主串。相对比较暴力方法(一个一个字符进行比较)的时间复杂度 O(MN),KMP算法通过设定next数组而减少了匹配的趟数,能够将时间复杂度降至 O(N+M)节省了大量的时间。
简单举一个例子:
我们要在主串S:ababcabcacbab,中匹配模式串T:abcac
KMP的next数组我先直接写出来,具体怎么得到的,我们后面再讲:

在第一次匹配中,从首部开始匹配:i从0开始,j从0开始。当i=2,j=2时匹配失败,接下来我们查看next数组,next[2]=0,因此我们将模式串的第一位移动到此时j的位置上来,也就是T:abcac向右移动j - next [j] = 2 位

接下来是第二次匹配,i从2开始,j从0开始。当i=6,j=4时匹配失败,此时i不动,此时next[4]=1,因此我们将模式串的第二位移动到此时j的位置上来,也即是模式串T要相对于主串S向右移动j - next [j] = 3位,j回溯到1
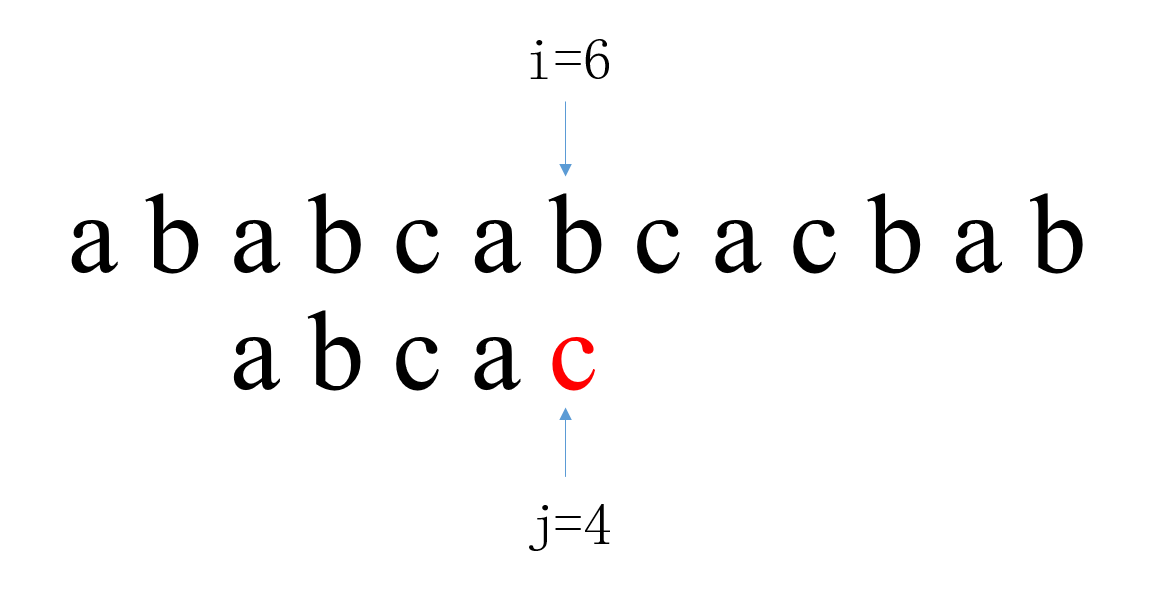
第三次匹配中,i从6开始,j从1开始。当i=10,j=5时匹配成功,返回i - j = 5,也即是在主串的第六位能够匹配成功。
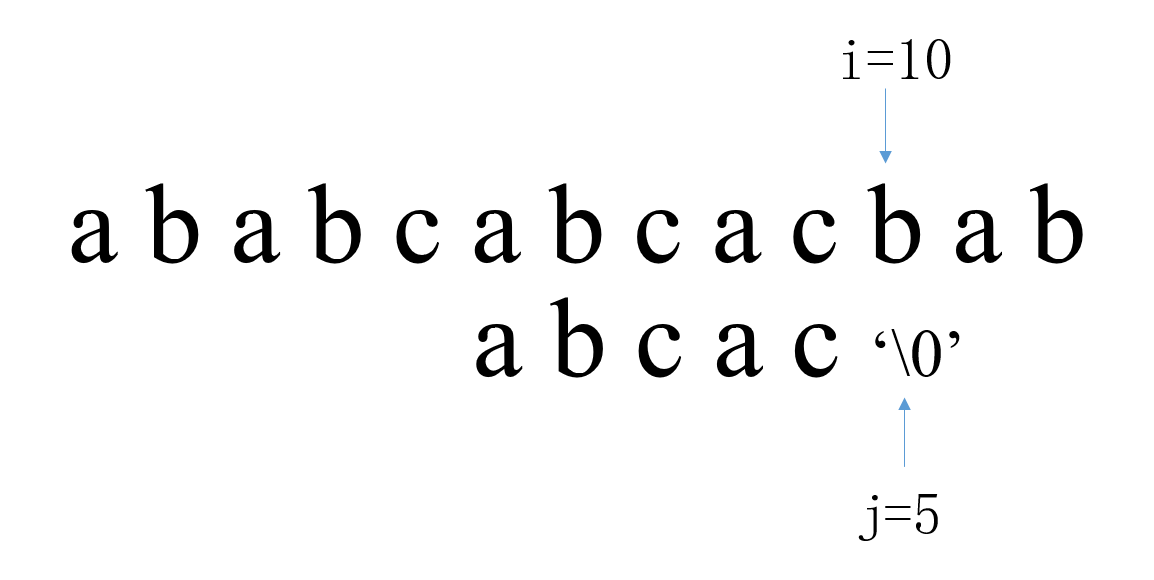
KMP的代码实现:
通过上述例子,我们已经知道KMP主要是通过Next数组的值而进行字符串的前进,而减少匹配的趟数,可以根据此写出代码:
def KMP(word,string,next):
i=0
j=0
while(i<len(word) and j<len(string)):
if(j==-1 or word[i]==string[j]):
j+=1
i+=1
else:
j=next[j]
if j==len(string):
return True
else:
return False
那么next数组该如何得出呢?
next数组是通过最长公共前后缀得出的。什么是最长公共前后缀呢?
- 规则如下:
那么如何寻找前后缀呢?
-
找前缀时,要找除了最后一个字符的所有子串。
-
找后缀时,要找除了第一个字符的所有子串。
下面举一个例子来说明如何寻找最大公共前后缀:
假设有串p=abaabca,各个子串的最大公共前后缀长度如下表所示:
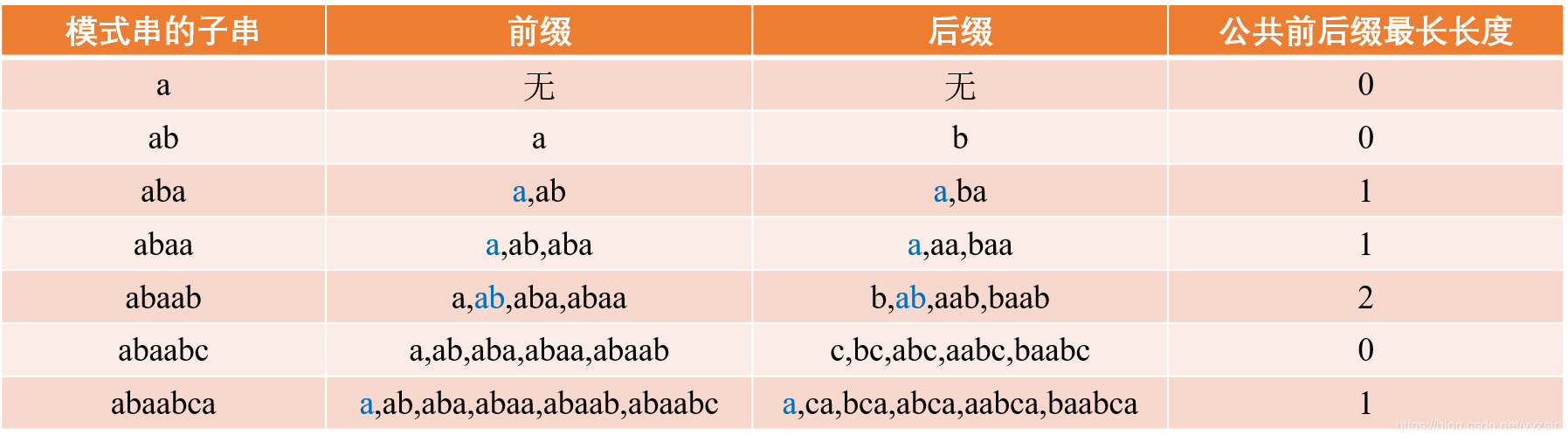
公共前后缀最长长度就会和串P的每个字符产生一种对应关系:

接下来我们就用这个表来引出next数组,next 数组的值是除当前字符外(注意不包括当前字符)的公共前后缀最长长度,相当于把上表做一个变形,将表中公共前后缀最长长度全部右移一位,第一个值赋为-1。

next数组的代码实现:
def getNext(b):
#时间复杂度较高
c=[-1,0]
for i in range(2,len(b)):
a=b[0:i]
res = 0
for time in range(1,len(a)):
if(a[0:time]==a[len(a)-time:len(a)]):
res=time if time>res else res
c.append(res)
return c
以上的代码是根据上节所述得出的步骤而得出的,虽然易于理解,但是可以看出时间复杂度较高达到了 O(NlogN),非常的高,我们可以在此基础上进行优化(参考文章):
假定我们给定了某模式串,且已知next[j] = k,现在求得next[j+1]等于多少。
我们分两种情况分析:
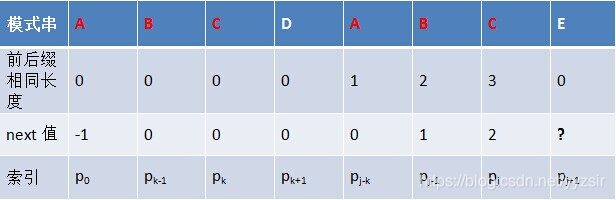
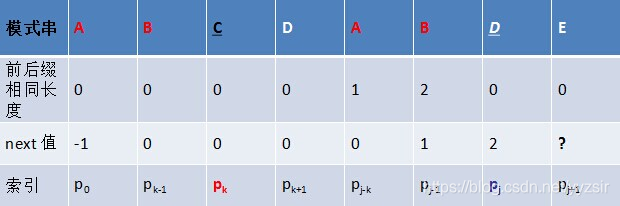
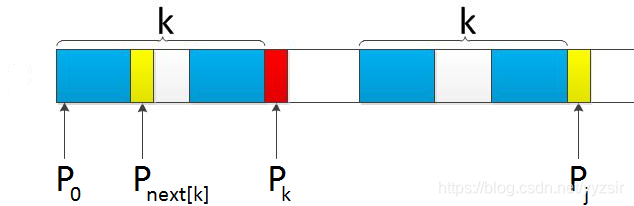
综上,优化后的代码如下:时间复杂度降为O(N)
def getNext(b):
j=0
k=-1
next=[-1 for i in range(len(b))]
while(j<len(b)-1):
if(k==-1 or b[j]==b[k]):
k+=1
j+=1
next[j]=k
else:
k=next[k]
return next
AC自动机的实现:
在介绍完成了字典树和KMP后,其实AC自动机就是将这两个方法进行结合。
其核心算法仍是寻找模式串内部规律,进行每次失配的高效跳转。这点和KMP算法一致,不同点在于,AC自动机寻找模式串的相同前缀。
AC自动机使用前缀树来存放所有模式串的前缀,通过失配指针来处理失配的跳转。AC自动机的构建,首先需要构建Trie树,其次需要添加失配指针(fail表),最后需要模式匹配。下图是用单词her、say、she、shr、he构成的AC自动机。
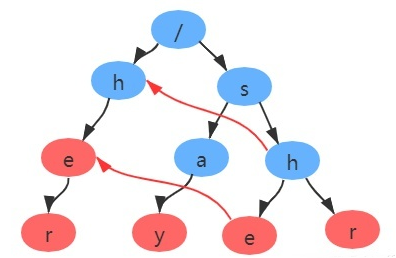
构建过程:
- 第一步:构建一个字典树:
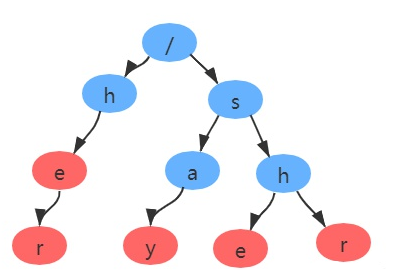
构建fail表之前,我们需要明确,每个节点:父节点、子节点列表、fail节点、节点的值和是否是尾节点这几个属性组成:
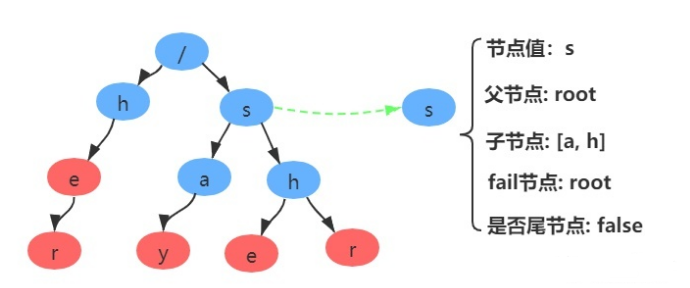
-
第二步:构建fail表:
fail表中保存了fail指针,fail指针就是当前位置失配以后能够跳转继续进行匹配的字符位置,达到匹配过程中不需要回溯的效果。构建过程使用了BFS(宽度优先搜索)算法。
假设当前节点为temp, 我们找到temp的父节点,得到父节点的fail节点,再找到fail节点的所有子节点,寻找子节点中是否有和temp节点值相同的节点,若存在则temp的fail节点指向该节点,如不存在继续寻找该fail节点的fail节点,直到找到与相同值的节点或达到root节点。
举例:
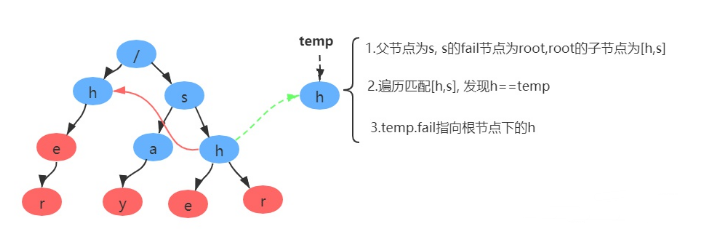
通俗来讲:就是在匹配了s->h后 观察h的上层是否含有h的结点,若存在则进行比较该h结点后至结束节点r和上一层的h节点值结束结点r的长度,若上层r长度较长则指向上层r;若不存在则指向根节点
因此,最终我们得到的fail指针如图所示:
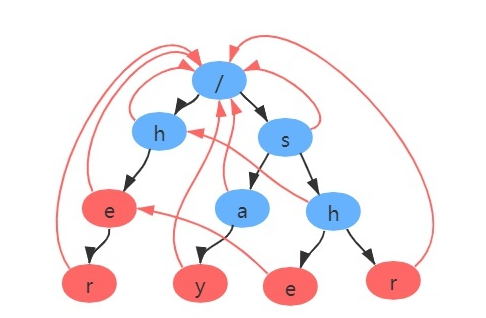
-
第三步:模式匹配
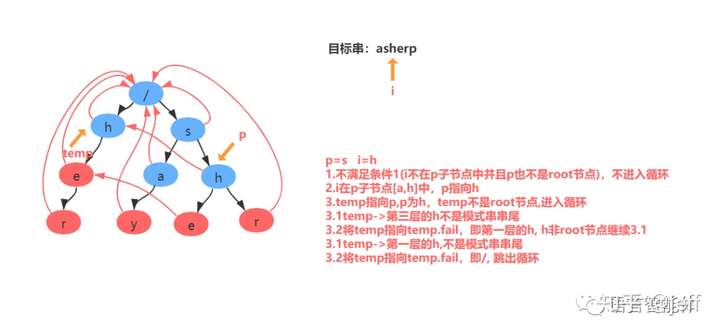
匹配的核心是从目标串从头逐个开始,在ac自动机中进行匹配,匹配上的则计数,若未匹配上则跳转失配位置进行尝试匹配,直到全部匹配完成。
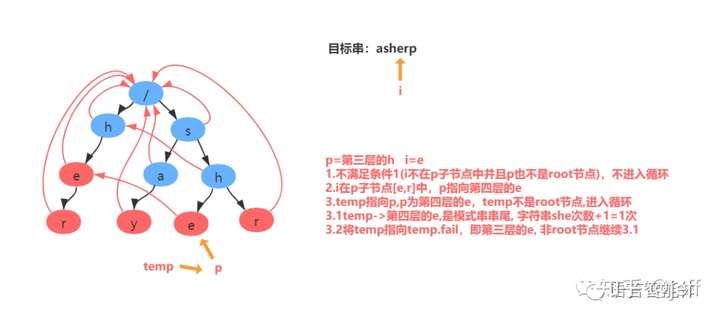
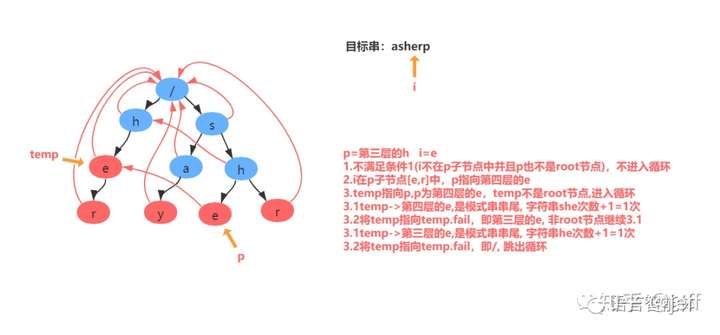
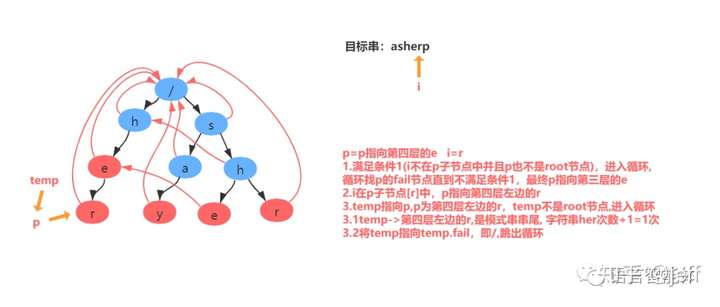
举例:匹配目标串asherp
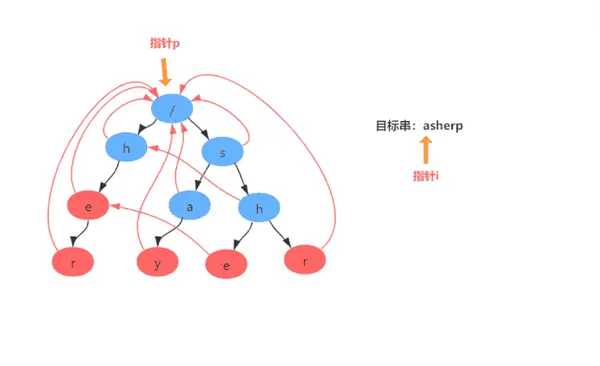
匹配过程分解: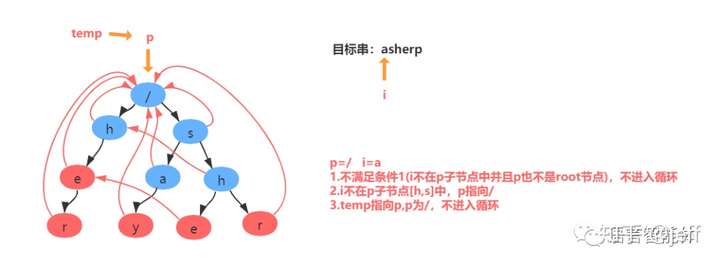
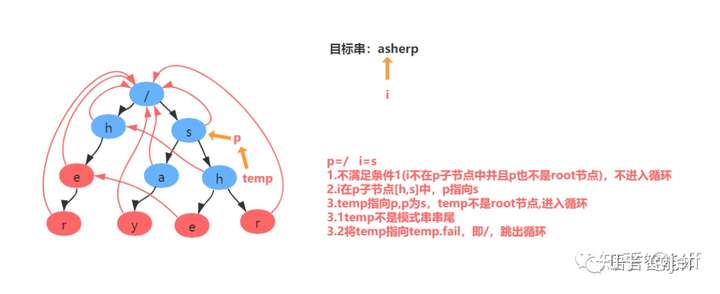
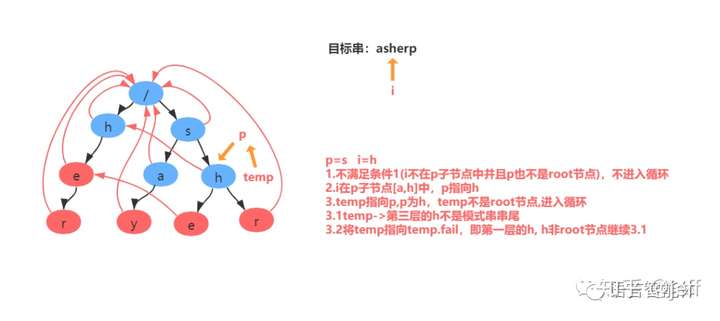
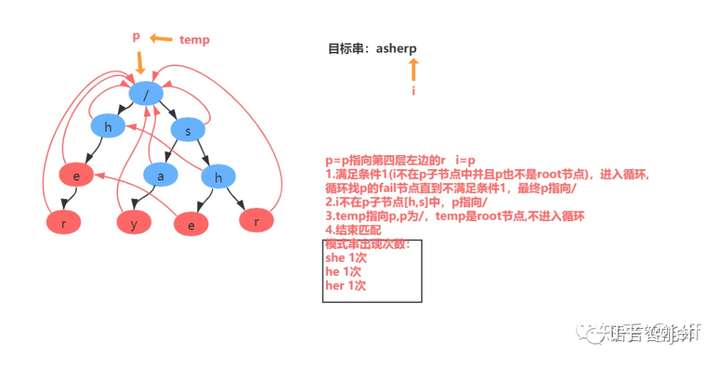
AC自动机代码实现:
class node:
def __init__(self,char):
self.char=char
self.fail=None
self.tail=0 #尾标志
self.child=[] #子结点
self.childValue=[] #子结点的值
class ACmation:
def __init__(self):
self.root=node("") #根节点
self.count=0
def Insert(self,strKey):
self.count+=1
p=self.root
for i in strKey:
if i not in p.childValue:
child=node(i)
p.child.append(child)
p.childValue.append(i)
p=child
else:
p=p.child[p.childValue.index(i)] #否则,转到该子结点
p.tail=self.count
#修改fail指针
def acAutomation(self):
p=[self.root] #列表代替队列
while len(p): #BFS
temp=p[0]
p.remove(temp)
for i in temp.child: #开始遍历子节点
if temp==self.root: #若根的子结点fail指向自己
i.fail=self.root
else:
q=temp.fail
while q:
if i.char in q.childValue: #如果在子结点中匹配则指向该子结点
i.fail=q.child[q.childValue.index(i.char)]
break
q=q.fail #否则继续循环
if q==None: #如果没出现过就放到根结点
i.fail=self.root
p.append(i) #将当前结点的子结点放入队列
#模式匹配
def runkmp(self,strMode):
p=self.root
cnt={} #record the state of successful
for i in strMode:
while i not in p.childValue and p is not self.root:
p=p.fail #若字符不在子节点中且不为根节点,循环
if i in p.childValue: #找到了就指向那个结点否则就指向根节点
p=p.child[p.childValue.index(i)]
else:
p=self.root
temp=p
while temp is not self.root: #若此结点不为根节点且fail存在则匹配成功
if temp.tail:
if temp.tail not in cnt:
cnt.setdefault(temp.tail)
cnt[temp.tail]=1
else:
cnt[temp.tail]+=1
temp=temp.fail
return cnt
ac=ACmation()
dic=['南京','南京市','长江','大桥','长江大桥']
for i in dic:
ac.Insert(i)
ac.acAutomation()
print(ac.runkmp("南京市长江大桥"))
{1: 1, 2: 1, 3: 1, 5: 1, 4: 1}
# 数字含义:数组下标:出现次数
#南京1次,南京市1次,长江1次,长江大桥1次,大桥1次