威伦特

本文介绍的是基于统计的中文分词的方法。

语言模型：

语言模型(Language Model，LM)指的就是对语言珍象的数学抽象。确切来讲，给定一个句子w，语言模型就是计算句子的出现概率p(w)的模型我们无法枚举全人类在过去、现在和将来生成的所有句子，只能采样一个小型的样本空间，程为语料库。于是，这个概率分布就统计自某个人工标注而成的语料库。

$p(w)=p(w_1|w_0)*p(w_2|w_0w_1)*...*p(w_{k+1}|w_0w_1w_2...w_k)$

$w_0=句子的开头\\w_1=句子第一个词语\\w_k+1=句子的结束\\ 句子=w_1w_2w_3...w_k$

---

$Example:\\ Corpus：\\商品，和，服务；\\商品，和服，物品；\\服务，和，货币$

$Sentence:w=商品，和，服务$

$p(商品,和,服务)=p(商品|w_0)*p(和|商品，w_0)*p(服务|和，商品,w_0)*p(w_{k+1}|商品，和，服务,w_0)\\=2/3*1/2*1/1*1/1\\=1/3$

马尔可夫链与二元语法

在语言模型的基础上假设该词出现的概率被前一个词所决定

$p(w_t|w_0w_1...w_{t-1})=p(w_t|w_{t-1})$

因此语言模型公式可简化为：

$p(w)=p(w_1|w_0)*p(w_2|w_1)*...*p(w_{k+1}|w_k)$

---

$Continue\ the \ example \ of \ previous \\ p(商品,和,服务)=p(商品|w_0)*p(和|商品)*p(服务|和)*p(w_{k+1}|商品)\\ =2/3*1/2*1/2*1/1\\ =1/6$

这样缓解了数据稀疏的问题

n元语法

每个单词的概率仅取决于改单词前的n个单词

马尔可夫链与二元语法就是n=2的情况

数据稀疏与平滑策略

当数据太过于稀疏的时候，可以利用低阶n元语法平滑高阶n元语法。

例如：线性插值法

$p(w_t|w_{t-1})=a*p_{ML}(w_t|w_{t-1})+(1-a)p(w_t)$

---

$Example:\\a=0.5\\p(和)=0.5\\ p(和| 商品)=0.5*1/2+0.5*0.5\\=1/2$

实例：通过二元语法模型来分词

导入语料库：

Corpus：

• 商品，和，服务
• 商品，和服，物品
• 服务，和，货币

构建图

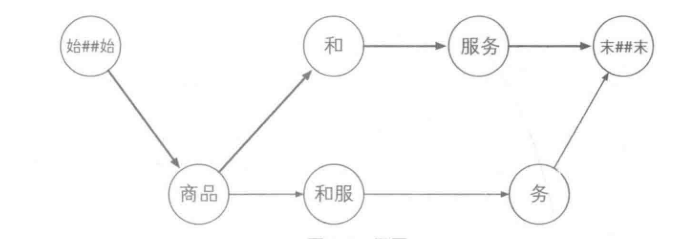
通过平滑策略计算结点之间的距离

中文分词常用的经验公式：

$p(w_t|w_{t-1})=a*[(b*\frac{c(w_{t-1}w_t)}{c(w_t)}+1-b]+(1-a)\frac{c(w_t)+1)}{N} \\a，b为不同的平滑因子$

由于多个0~1之间的数连续相乘会使值接近或者等于0，因此需要对概率进行取负对数

$\prod_{i = 1}^{k+1}{p(w_t|w_{t-1})}=-\prod_{i = 0}^{k+1}log{p(w_t|w_{t-1})}$

结果如下：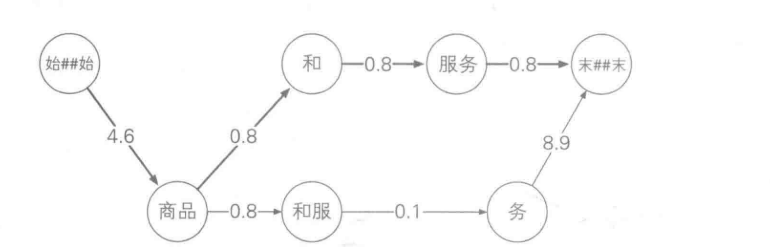

寻找最短距离

常见的最短距离算法有DS中的Dijkstra，Floyd算法，在NLP中：由马尔科夫链构成的网状图的最短距离算法使用维特比算法。

接下来介绍维特比算法（转于知乎:如何通俗地讲解 viterbi 算法)

什么是维特比算法

维特比（Viterbi）算法属于一种动态规划算法，目标在于寻找最优路径。

维特比算法图解

从S和E之间找一条最短的路径

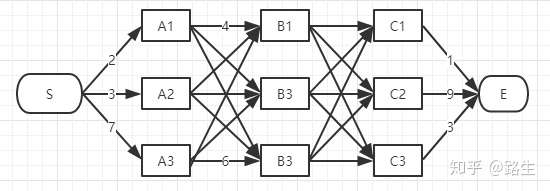
为了找出S到E之间的最短路径，我们先从S开始从左到右一列一列地来看。

首先起点是S，从S到A列的路径有三种可能：S-A1、S-A2、S-A3，如下图：

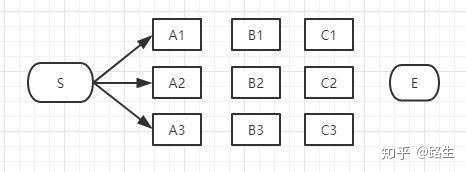
​ 我们不能武断地说S-A1、S-A2、S-A3中的哪一段必定是全局最短路径中的一部分，目前为止任何一段都有可能是全局最短路径的备选项。

我们继续往右看，到了B列。按B列的B1、B2、B3逐个分析。

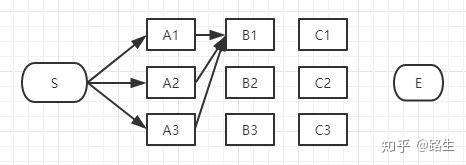
以上这三条路径，各节点距离加起来对比一下，我们就可以知道其中哪一条是最短的。假设S-A3-B1是最短的,那么其余两条就可以删掉了，用相同方法依次比较B2和B3，得出到B1，B2，B3的最短路径

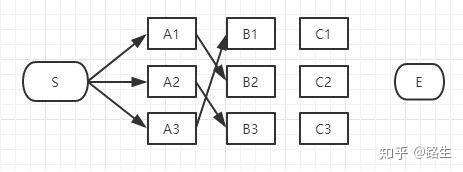
接下来到C列了，类似上面说的B列，我们仍然从C1、C2、C3一个个节点分析。方法和B相同，

假设结果如下。

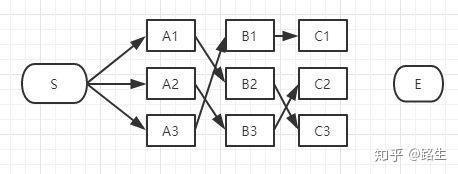
接下来只需要计算C1，C2，C3到E的路径谁最小就行了

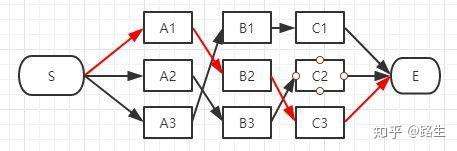
在效率方面相对于粗暴地遍历所有路径，viterbi 维特比算法到达每一列的时候都会删除不符合最短路径要求的路径，大大降低时间复杂度。

计算结果

经过维特比算法后，输出为

['','商品','和','服务'，'']

总结：

基于统计的方法能够较好的切分歧义和识别新词，目前受到了研究者越来越多的重视。不受待处理文本的领域限制，不需要特定的词典，能够有效的自动排出歧义，较好的识别未登录词。缺点是需要大量的训练文本用于建立统计模型的参数，方法的计算量较大，对于常用词的识别精度差，且分词精度和训练文本的选择有关，会存在一些共现频度高但是并不是词的常用字组。