隐马尔可夫模型

隐马尔可夫模型（Hidden Markov Model，HMM）是描述两个时序序列联合分布p(x,y)的概率模型。

x序列外界可见（外界指的是观测者)，称为观测序列( observation sequence ) ; y序列外界不可见，称为状态序列( state sequence )。

隐马尔可夫模型之所以称为“马尔可夫模型”，是因为它满足马尔可夫假设。

马尔可夫假设：每个事件的发生概率只取决于前一个事件。

隐马尔可夫模型：①\ 它的马尔可夫假设作用于状态序列。假设当前状态 y_t 只依赖于前一个状态 y_{t-1} \\ ②\ 任意时刻观测x_t只依赖于该时刻的y_t,于其他时刻的状态和观测无关

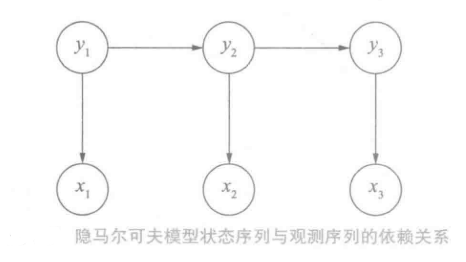
为什么x可以决定y呢？因为在概率论中：联合概率分布p(x,y)中\\ p(x,y)=p(x)p(y|x)=p(y)p(x|y)\\

隐马尔可夫模型利用了三个要素来模拟时序序列的发生，分别为初始状态概率向量、状态转移概率矩阵和发射概率矩阵（观测概率矩阵）

初始状态概率向量

模型启动进入y_1称之为初始状态，假设y∈\{s_1,...,s_n\}，y_1就是一个独立的离散随机变量，\\ 通过p(y_1|\pi)表示，其中:\\ \pi=(\pi_1,...,\pi_N)^T,0<=\pi_i<=1，\sum^\N_{i=1}\pi_i=1\\ \pi称之为初始状态概率向量

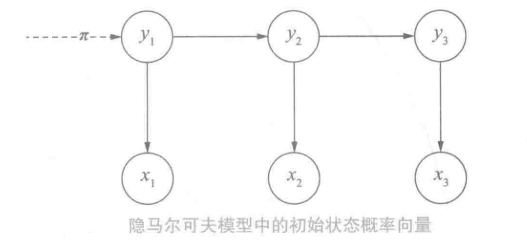
在给定了初始状态概率向量，初始状态y_1的取值分布就可以确定了。

举个例子：在中文分词中，采用{B,M,E,S}标注集的时候。

什么是{B,M,E,S}标注集：

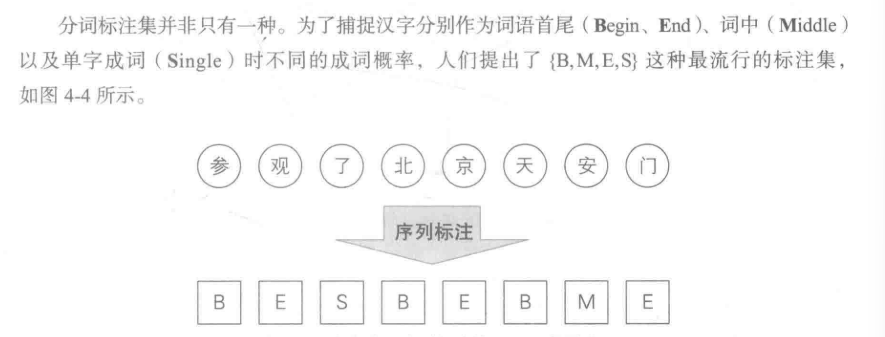
中文分词的例子中，在句子开头不可能是词语中间或词语结尾，只能是词语开头和单字成词，因此其初始状态概率向量可能如下：

P(B) = 0.7\ P(M) = 0\ P(E) = 0\ P(S) = 0.3

那么y的所有可能的取值和概率就可以被计算出来：

p(y_1=B)=0.7\\ p(y_1=M)=0\\ p(y_1=E)=0\\ p(y_1=S)=0.3\\ 此时的隐马尔可夫模型的初始状态概率向量为:[0.7,0,0,0.3]

状态转移概率矩阵

状态转移概率矩阵的确定过程：

在确定了y_t后根据马尔可夫假设，可以将y_t转移到y_{t+1}。因为y_t一共有N种假设状态，\\ 那么从状态\ a->b\ 的概率就构成了N*N的矩阵，该矩阵称之为状态转移概率矩阵A\\

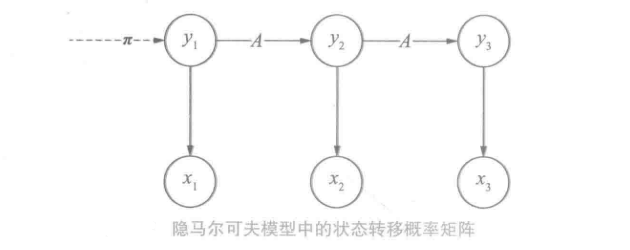
在中文分词中，标签B的后面不可能是S，于是只需赋予\\ p(y_{t+1}=S|y_t=B)=0就可以模拟这种禁止转移的需求。\\ 此外，汉语中的长词相对较少，于是隐马尔可夫模型可以通过\\ 减少p(y_{t+1}=M|y_t=M)来模拟该语言现象。\\同样，词性标注中的“形容词→名词”“副词→动词”也可以通过状态转移概率来模拟。\\ 这些概率分布的参数都不需要手动赋予，而是通过语料库上的统计自动学习。

发射概率矩阵

有了状态y之后那么怎么确定对应的观测x的概率分布呢？

这时根据隐马尔可夫假设②任意时刻观测x只依赖于该时刻的y,于其他时刻的状态和观测无关。若观测x一共有M种可能，那么x的概率分布参数向量的维度为M。由于y一共有N种，那么这些参数构成了N*M矩阵(size(状态) * size(x))，成为发射概率矩阵B。

例如：我们决定矩阵B中第一行表示字符集中的“阿”，\\此时 p(x_1=阿|y_1=B)对应为矩阵中左上角的第一个元素。\\若字符集的大小为1000，那么size(B)=4*1000\\ 注意：y_1=B代表为y_1为词语开头

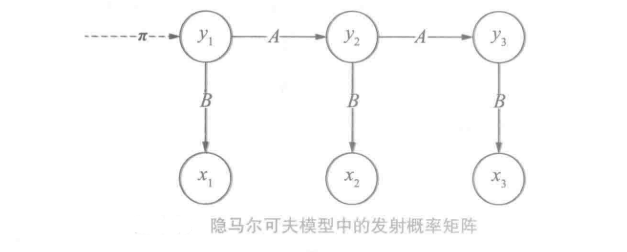
初始状态概率向量、状态转移概率矩阵与发射概率矩阵成为隐马尔可夫模型的三元组。三元组确定后，隐马尔可夫模型就确定了。

隐马尔可夫模型的三个基本用法

样本生成问题：给定模型三元组，生成满足模型约束的样本。
模型训练问题：给定训练集，估计模型三元组参数
序列预测问题：已知模型三元组参数，给定观测序列x，求最可能的状态y

样本生成问题实例

设想如下案例:

某医院招标开发“智能”医疗诊断系统，用来辅助感冒诊断。

①来诊者只有两种状态:要么健康，要么发烧。
②来诊者不确定自己到底是哪种状态，只能回答感觉头晕、体寒或正常。
③感冒这种病，只跟病人前一天的状态有关。
④当天的病情决定当天的身体感觉。

有位来诊者的病历卡上完整地记录了最近T天的身体感受(头晕、体寒或正常)，请预测这T天的身体状态（健康或发烧)。

由于医疗数据属于机密隐私，医院无法提供训练数据，但根据医生经验，感冒发病的规律如图所示。

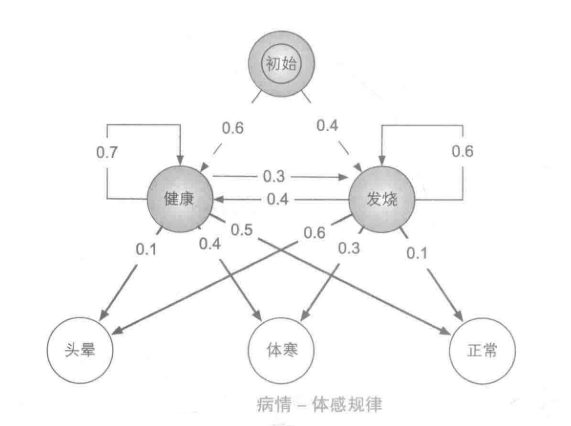
也就是说，在初始状态下有0.4的概率第二天发烧，然后有0.1的概率正常。

我们可以写出隐马尔可夫模型：

初始概率向量π：

【0.6，0.4】

状态转移概率矩阵A：

0.7	0.3
0.4	0.6

发射概率矩阵B：

0.5	0.4	0.1
0.1	0.3	0.6

样本生成：

生成过程就是沿着隐马尔可夫链走T步。

$① \ 根据π采样第一个时刻的状态，y_1=s_i$
$②\ y_t得到s_i后，根据A_i，采样下一时刻的状态y_{t+1}$
$③\ 对y_t=s_i，根据B_i采样x_t$
$④\ 重复（2）T-1次，重复（3）T次，输出x，y$

代码：

import random
pi=[0.6,0.4]
y=['健康','发烧']
x=['头晕','体寒','正常']
A=[[0.7,0.3],
   [0.4,0.6]]
B=[[0.5,0.4,0.1],
   [0.1,0.3,0.6]]
size=4
def generateHMM(status,size):
    symList=[0 for i in range(size)]
    symList[0]=x[status]
    initSym=0 if random.random()<=pi[0] else 1
    for i in range(1,size):
        symList[i],initSym=continueGen(initSym,i)
    print(symList)
def continueGen(now,i):
    if i==size-1:
        return y[now],0
    else:
        flag=random.random()
        genx= 1 if flag>=A[now][0] else 0#下一代的病情
        flag=random.random()
        if flag<=B[now][0]:
            return str(y[now]+" "+x[0]),genx
        elif flag<=(B[now][1]+B[now][0]):
            return str(y[now]+" "+x[1]),genx
        else:
            return str(y[now]+" "+x[2]),genx
generateHMM(0,4)
generateHMM(1,4)
generateHMM(2,4)

输出如下：

['头晕', '发烧 正常', '健康 体寒', '健康']
['体寒', '发烧 正常', '发烧 正常', '发烧']
['正常', '健康 头晕', '发烧 正常', '发烧']

由于随机数的原因，每次运行的结果都是随机的。

模型训练问题实例

通过上述样本来进行监督学习来估计模型参数。

在监督学习中，通过利用极大似然法来估计隐马尔科夫模型的参数。

初始状态概率向量的估计：

初始状态其实可以看作状态转移的一种特例，即y_1是由BOS转移而来。\\ 统计y_1的所有取值的频次记作向量c，然后用类似的方法归一化:\\ \hat{\pi}_{i}=\frac{c_{i}}{\sum_{i=1}^{N}c_{i}}\ ,\ i=1,2,...N

转移概率矩阵的估计：

样本若在t时刻处于状态s_i，在t+1时刻转移到s_j。统计这样的转移频次计入矩阵A_{i,j}，\\ 根据极大似然估计进行归一化：\\ \hat{a}_{i,j}=\frac{A_{i,j}}{\sum_{j=1}^{N}A_{i,j}}\ i,j=1,2,...N

发射概率矩阵的估计：

状态S_i且观测为o_j的频次，计入矩阵B_{i，j},则s_i发射观测o_j的概率为：\\ \hat{b}_{ij}=\frac{B_{i,j}}{\sum_{J=1}^{M}B_{i,J}}\ ,\ i=1,2,...N,j=1,2...,M

模型预测问题实例

给定了如下模型参数，计算观测状态序列“干燥，潮湿，干燥”的概率

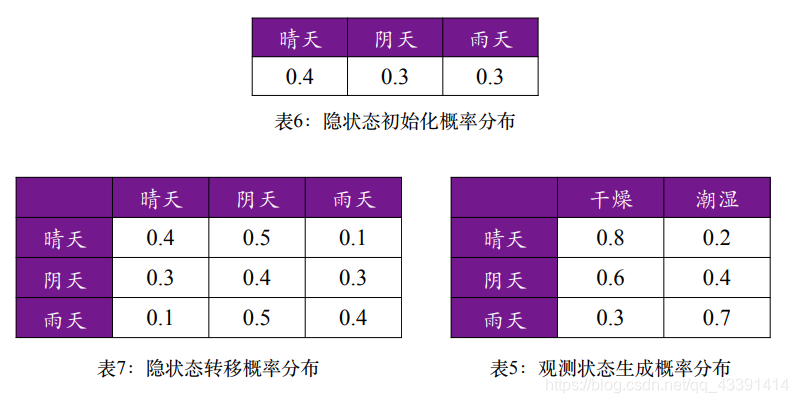
通过使用向前算法和维特比算法

动态规划——前向算法

循序渐进地解决问题，先不考虑最大概率的问题。给定观测序列x和一个状态序列y,两者的联合概率p(x,y)最大概率就是对所有(x,y)的搜索。

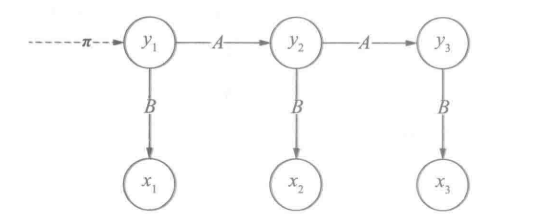
顺着隐马尔可夫链走，首先t =1时初始状态没有前驱状态，其发生概率由π决定，即:

p(y_1=S_i)=\pi_i\ ...①

接着对t>=2，y由前驱状态转移而来，概率由A决定，于是：

p(y_t=S_j|y_{t-1}=s_i)=A_{i,j}\ ...②

所以状态序列的概率为①②乘积：

p(y)=p(y_1,...,y_T)=p(y_1)\prod_{t=2}^{T}p(y_t|y_{t-1})

由于，每个y=s，都会发射一个x=o，发射概率由B决定：

p(x_t=O_j|y_t=s_i)=B_{i,j}\ ...③

那么给定长为T的状态序列y，对应x概率为③的累计形式：

p(x|y)=\prod_{t=1}^{T}p(x_t|y_{t})\ ...④

②④相乘得到显隐状态序列的联合概率：

p(x,y)=p(y_1)\prod_{t=2}^{T}p(y_t|y_{t-1})\prod_{t=1}^{T}p(x_t|y_{t})

最后将每个x，y对应实际发生的序列s，o，就能够带入三元组中的相应元素，计算出任意序列的概率。

根据例子：

首先求：\\ P（晴天，干燥）=\pi（晴天）*B（晴天，干燥）=0.32 \\p（阴天，干燥）=\pi（阴天）*B（阴天，干燥）=0.18\\ p（雨天，干燥）=\pi(雨天)*B(雨天，干燥)=0.09\\ 接下来求：\\P（潮湿，晴天|T_1=干燥）=（0.32*0.4+0.18*0.3*0.09*0.1）*0.2=0.382\\ P（潮湿，阴天|T_1=干燥）=（0.32*0.5+0.18*0.4+0.09*0.5）*0.4=0.1108\\ P(潮湿，雨天|T_1=干燥）=（0.32*0.1+0.18*0.3+0.09*0.4）*0.7=0.0854 \\依此类推：\\ P(干燥，晴天|T_1=干燥,T_2=潮湿)=0.0456\\ ...

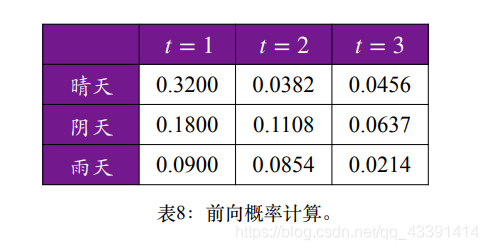
结果如表中所示：

那么“干燥、潮湿、干燥” 的概率为：

P=0.0456+0.0637+0.0214=0.1307

维特比算法

在构成了图后，接下来使用维特比算法寻找最优的状态序列：

在上面的表格例子中：

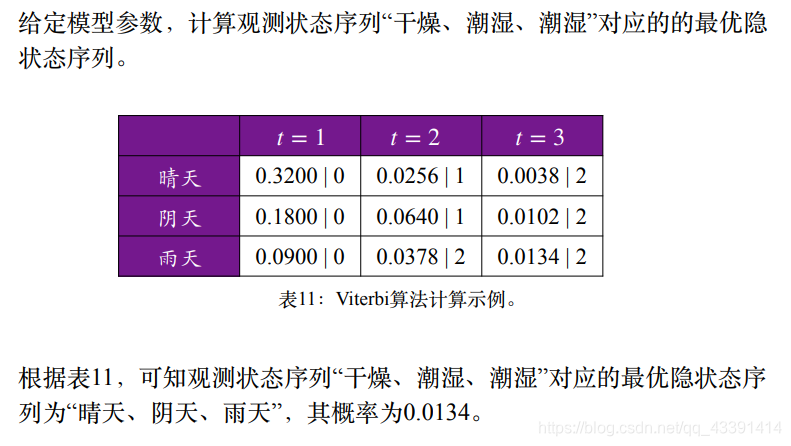
HMM应用于中文分词

大体步骤为：

用{B,M,E,S}进行标注
语料转换为二元组（x，y），也就是字符:{B,M,E,S}标签
使用HMM训练

在hanlp中已经实现了HMM分词器，因此可以直接使用API进行调用：

from pyhanlp import *
FirstOrderHiddenMarkovModel = JClass('com.hankcs.hanlp.model.hmm.FirstOrderHiddenMarkovModel')
HMMSegmenter = JClass('com.hankcs.hanlp.model.hmm.HMMSegmenter')
def train(model):
    segmenter = HMMSegmenter(model)
    segmenter.train('./msr_training.utf8')
    print(segmenter.segment('商品和服务'))
    return segmenter.toSegment()
if __name__ == '__main__':
    segment = train(msr_train, FirstOrderHiddenMarkovModel())

[商品, 和, 服务]#output

总结

HMM隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态的序列，再由各个状态随机生成一个观测从而产生观测序列的过程。

HMM 应用在中文分词问题

如果有标注语料，则问题的解决过程：

计算初始状态概率分布
计算转移概率矩阵
计算输出概率矩阵
使用 Viterbi 算法解码

如果没有标注语料，则问题的解决过程：

获取词的个数
确定状态的个数
参数学习（利用 EM 迭代算法获取初始状态概率、状态转移概率和输出概率）
使用 Viterbi 算法解码

威伦特