威伦特

解码生命

首页 文章 标签 关于

文本聚类算法及其实现

2022-08-23 12 min read # NLP

聚类分析在文本分析、商务应用、网页搜索、推荐系统、生物医学等多个领域都有着十分广泛的应用。

聚类是一种无监督学习方式，目的是把一个数据根据某种规则划分为多个子数据，一个子数据就称为一个聚类。

目前聚类主要分为以下几类：

  • 基于划分的聚类算法
  • 基于密度的聚类算法
  • 基于层次的聚类算法
  • 基于网格的聚类算法
  • 基于模型的聚类算法

文本聚类的基本流程：

  • 特征提取
  • 向量聚类

如果能将文档表示为向量，就可以对其应用聚类算法。这种表示过程称为特征提取，而一旦将文档表示为向量，剩下的算法就与文档无关了。

文档的特征提取

词袋模型

词袋(bag-of-words )是NLP中最常用的文档表示模型，它将文档想象为一个装有词语的袋子， 通过袋子中每种词语的计数等统计量将文档表示为向量。比如下面的例子:

人 吃 鱼。
美味 好 吃！

统计词频后如下:

人=1
吃=2
鱼=1
美味=1
好=1

那么两个句子就可以向量化，这 5 个维度分别表示这 5 种词语的词频。

[1,2,1,0,0]
[0,2,0,1,1]

词袋模型不考虑词序，也正因为这个原因，词袋模型损失了词序中蕴含的语义，比如，对于词袋模型来讲，“人吃鱼”和“鱼吃人”是一样的，这就不对了。

词袋中的统计指标

词袋模型并非只是选取词频作为统计指标，而是存在许多选项。常见的统计指标如下:

  • 布尔词频: 词频非零的话截取为1，否则为0，适合长度较短的数据集
  • TF-IDF: 适合主题较少的数据集
  • 词向量: 如果词语本身也是某种向量的话，则可以将所有词语的词向量求和作为文档向量。适合处理 OOV 问题严重的数据集。
  • 词频向量: 适合主题较多的数据集

这里选用词频作为统计指标，向量d具体表示如下：

di=(TF(t1,di),TF(t1,di),...,TF(tj,di))d_i=(TF(t_1,d_i),TF(t_1,d_i),...,TF(t_j,d_i))

t代表单词，TF（t，d）表示单词t在文档d中的次数，同时将该向量处理为单位向量

文本的向量化转换已经完成了，接下来就可以运用各类聚类算法进行计算了

聚类算法

基于划分的算法——K均值算法

K均值算法的思想是：

1.在数据集中随机选取K个样本作为簇的中心，然后计算其他样本离这K个簇中心内的距离。

2.将每个样本划分到与其距离最近的簇中心所在的簇中。

3.将簇中所含样本的距离均值作为新的簇中心。

4.再根据新划分的簇中心来计算每个样本离簇中心的距离。

5.迭代计算，直到簇中心在每次迭代后变化不大。

img

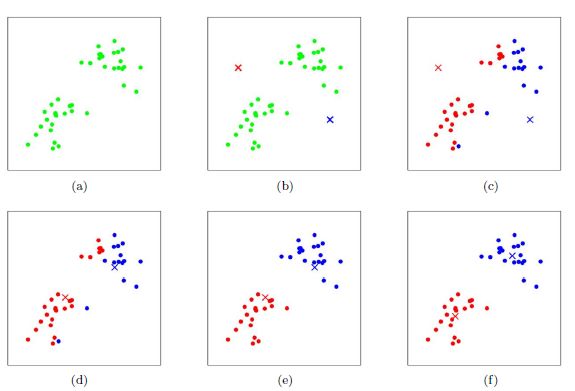
距离的计算可以采用欧式距离，余弦距离。

假设n为空间有两点a=(x1,x2,...,xn)b=(y1,y2,...,yn)那么n维空间两点的欧式距离为：假设n为空间有两点\\a=(x_1,x_2,...,x_n)\\ b=(y_1,y_2,...,y_n)\\ 那么n维空间两点的欧式距离为：

D=∑k=1n(xk−yk)2余弦距离为：cos=a.b∣a∣∣b∣D=\sqrt{\sum_{k=1}^n(x_k-y_k)^2} \\余弦距离为： \\cos=\frac{a.b}{|a||b|}

实现

HanLP 中，聚类算法实现为 ClusterAnalyzer。

假设该音乐网站将 6 位用户点播的歌曲的流派记录下来，并且分别拼接为 6 段文本。给定用户名称与这 6 段播放历史，要求将这 6 位用户划分为 3 个簇。实现代码如下:

from pyhanlp import *

ClusterAnalyzer = JClass('com.hankcs.hanlp.mining.cluster.ClusterAnalyzer')

if __name__ == '__main__':
    analyzer = ClusterAnalyzer()
    analyzer.addDocument("赵一", "流行, 流行, 流行, 流行, 流行, 流行, 流行, 流行, 流行, 流行, 蓝调, 蓝调, 蓝调, 蓝调, 蓝调, 蓝调, 摇滚, 摇滚, 摇滚, 摇滚")
    analyzer.addDocument("钱二", "爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲")
    analyzer.addDocument("张三", "古典, 古典, 古典, 古典, 民谣, 民谣, 民谣, 民谣")
    analyzer.addDocument("李四", "爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 爵士, 金属, 金属, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲, 舞曲")
    analyzer.addDocument("王五", "流行, 流行, 流行, 流行, 摇滚, 摇滚, 摇滚, 嘻哈, 嘻哈, 嘻哈")
    analyzer.addDocument("马六", "古典, 古典, 古典, 古典, 古典, 古典, 古典, 古典, 摇滚")
    print(analyzer.kmeans(3))

结果

[[李四, 钱二], [王五, 赵一], [张三, 马六]]

基于密度的算法——DBSCAN

DBSCAN算法思想是：

1.从一个没有被访问过的任意起始数据点开始。这个点的邻域是用距离 ε（ε 距离内的所有点都是邻域点）提取的。

2.如果在这个邻域内有足够数量的点，则当前数据点成为新簇的第一个点。否则，该点将会被标记为噪声。在这两种情况下，该点都被标记为已访问。

3.对于新簇中的第一个点，其 ε 距离邻域内的点也成为该簇的一部分。并且对所有刚刚添加到簇中的新点进行重复。

4.迭代，直到簇中所有的点都被确定，即簇的 ε 邻域内的所有点都被访问和标记过。

5.当完成了当前的簇后，寻找另一个未访问的点，重复上诉操作。直到所有的点都已经被访问，每个点都属于某个簇或噪声。

img

实现

sklearn中DBSCAN对象重要参数如下:

  • eps：从一个观察值到另一个观察值得最远距离，超过这个距离将不再认为二者是邻居

  • min_samples：最小限度的邻居数量，如果一个观察值在其周围小于eps距离的范围内有超过这个数量的邻居，就被认为是核心观察值

  • metric：eps所用的距离度量，比如minkowski(闵可夫斯基距离)或者euclidean(欧式距离)。注意，如果使用闵可夫斯基距离，就可以用参数p设定闵可夫斯基中的幂次。

from sklearn.cluster import DBSCAN
import numpy as np
X = np.array([[1, 2], [2, 2], [2, 3],
              [8, 7], [8, 8], [25, 80]])
clustering = DBSCAN(eps=3, min_samples=2).fit(X)
print(clustering.labels_)

结果

array([ 0,  0,  0,  1,  1, -1]) #0，1代表两个簇，-1为噪点

基于层次的算法——AGNES，DIANA

AGNES 是一种自下向上层次聚类算法。

AGNES算法思想：

1、将每个样本当成一个初始簇
2、选择一个测量两个簇之间的距离，也就是第一个簇中的数据点与第二个簇中的数据点之间的平均距离。
4、将有最小距离的两个簇进行合并，生成新的簇的集合
5、直到达到定义的簇的数目

img

实现

sklearn中AGNES对象重要参数如下:

  • n_clusters:分裂的簇的数量。默认为2
  • affinity：所用的距离度量，例如cosine(余弦距离)或者euclidean(欧式距离)
  • distance_threshold：超过该链接距离阈值，集群将不会合并。默认为None。如果不为None，那么n_clusters 一定为 None 同时 compute_full_tree 为 True.
from sklearn.cluster import AgglomerativeClustering
import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0],
               [4, 2], [4, 4], [4, 0]])
clustering = AgglomerativeClustering().fit(X)
print(clustering.labels_)

输出

array([1, 1, 1, 0, 0, 0])

而DIANA与AGNES相反，它是先将所有样本置于一个簇中，将临近点中的最远距离的点进行分裂。直到最后达到设定的簇数

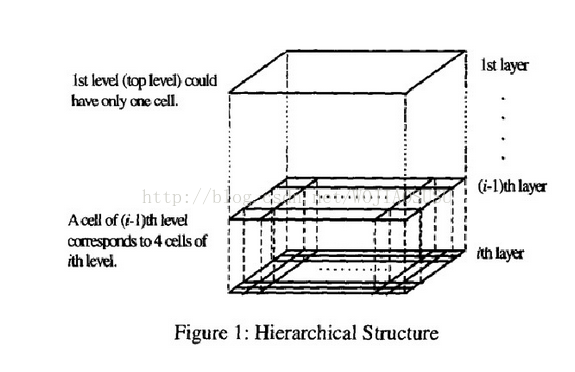
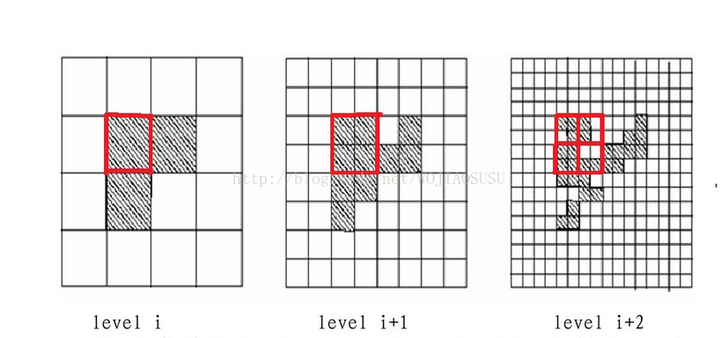
基于网格的聚类——STING

将空间区域划分为矩形单元。针对不同级别的分辨率，通常存在多个级别的矩形单元，同时高层的每个单元被划分为多个低一层的单元。根据单元属性的相关统计信息（例如平均值，最大值，和最小值）进行划分网格，而且网格也是分层次的，下一层是上一层的继续划分。高一层单元的统计参数可以很容易地从低层单元的参数计算出来。在一个网格内的数据点即为一个簇。

相关统计信息有：

  • 属性无关的变量 ：
    • count
  • 属性相关的变量 ：
    • m（平均值）
    • s（标准偏差）
    • min（最小值）
    • max（最大值）
    • 单元中属性值遵循的分布类型 distribution，例如正态的，均衡的，指数的，或无

数据被装载进数据库，最底层单元的变量 count，m，s，min，和 max 直接进行计算

算法思想：

1.在层次结构中选定一层作为查询处理的开始点。通常，该层包含少量的单元。

2.对当前层次的每个单元，我们计算置信度区间（或者估算其概率），用以反映该单元与给定查询的关联程度。不相关的单元就不再考虑。

3.对于相关单元，进行低一层的处理，这个处理过程反复进行，直到达到最底层。

4.此时，如果查询要求被满足，那么返回相关单元的区域。

5.若查询不满足，对相关单元进行检索数据和进一步的处理，直到它们满足查询要求

img
img

基于模型的聚类——高斯混合模型

K-means无法将两个均值相同（聚类中心点相同）的类进行聚类，而高斯混合模型（Gaussian Mixture Model, GMM）就是为了解决这一缺点而提出的

GMM概率密度函数：

P(x)=∑k=1Kp(k)p(x∣k)=∑k=1Kakp(x∣μk,∑k)P(x)=\sum_{k=1}^Kp(k)p(x|k)=\sum_{k=1}^Ka_kp(x|μ_k,\sum k)

其中，k：预先设定的簇的个数，ak为属于第k个簇的高斯概率，p(x|k)为第k个簇的高斯概率，均值向量为μk，Σk为协方差矩阵

算法思想：

1.设置簇k的个数，即初始化高斯混合模型的成分个数。（随机初始化每个簇的高斯分布均值和方差。也可观察数据给出一个相对精确的均值和方差）

  1. 计算每个数据点属于每个高斯模型的概率，即计算后验概率。（点越靠近高斯分布的中心，则概率越大，即属于该簇可能性更高）

  2. 计算 α,μ,Σ 参数使得数据点的概率最大化，使用数据点概率的加权来计算这些新的参数，权重就是数据点属于该簇的概率。

  3. 重复迭代2和3直到收敛。

实现

sklearn中GaussianMixture重要参数如下:

  • n_components：混合高斯模型个数，默认为 1
  • max_iter：最大迭代数，默认为100
  • tol：迭代停止阈值，默认为 0.001
import numpy as np
from sklearn.mixture import GaussianMixture
X = np.array([[1, 2], [1, 4], [1, 0], [10, 2], [10, 4], [10, 0]])
gm = GaussianMixture(n_components=2, random_state=0).fit(X)
label=gm.predict(X)
print(label)
probs=gm.predict_proba(X)
print(probs)

输出

[1 1 1 0 0 0] #簇
[[0. 1.]#每个元素在每个簇中的概率
 [0. 1.]
 [0. 1.]
 [1. 0.]
 [1. 0.]
 [1. 0.]]

总结

各种算法的使用场景

属于 @威伦特 RSS