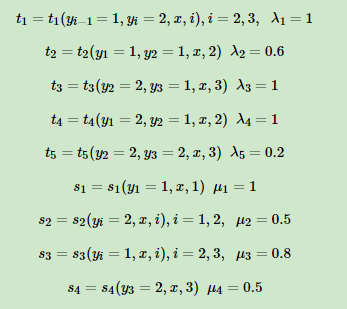威伦特

解码生命

首页 文章 标签 关于

条件随机场

2022-08-02 20 min read # 机器学习

条件随机场（conditional random field）是一个比感知机更加强大的模型。

背景知识

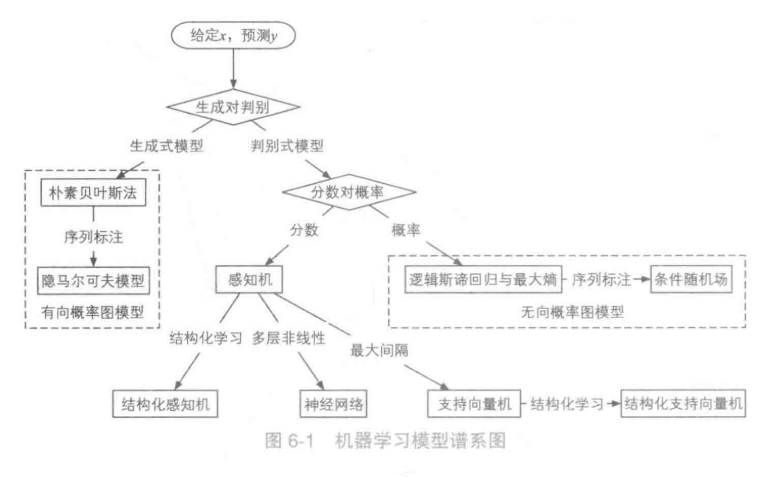
机器学习模型谱系图

Sklearn对应机器学习算法决策树
img
使用模板：
img

生成式模型

模拟数据的生成过程，且随机变量x，y存在因果先后关系：现有y再有x。这种关系通过联合分布模拟：

p(x,y)=p(y)p(x∣y)p(x,y)=p(y)p(x|y)

具体流程：

  • 根据p(y)采样y
  • 根据p(x|y)采用x
  • 生成样本概率p(x,y)
  • 通过遍历y的所有取值，获得最大的P(x,y)作为预测结果

通过p(x,y)，可以求得p(x)。

p(x)=∑y∈Yp(x,y)，Y为的取值p(x)=\sum_{y\in Y}p(x,y)，Y为的取值

但是，p(x)很难准确估计。因为特征之间并不是相互独立的，存在一定的依赖关系。

eg： 中文分词的一元语法：字符“榴”的后一个字符可以确定是“莲”，但是生成式模型直接认为这两个字符相互独立，忽略的这种依赖关系，导致不合符实际。

判别式模型

对生成式模型的改进。跳过了p(x)，直接对p(y|x)建模。这样不需要考虑x内的各种依赖关系。

在生成式和判别式中，模型都是多维度随机变量分布。这些随机变量可能相互独立，也可能相互依赖，可以通过概率图模型来进行分析多维随机变量分布。

有向和无向概率图模型

概率图模型

通过图来表示p(x,y)，利用结点来表示随机变量，用边来表示有关联的随机变量。

有向图模型

将事情通过前后因果顺序进行连接为有向图。

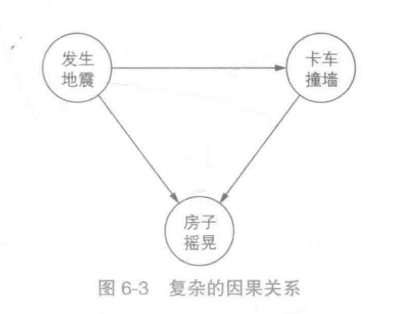
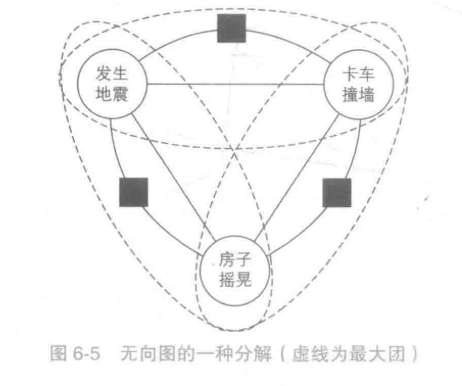
“发生地震”和“卡车撞墙”会导致“房子摇晃”，同时“发生地震”也会导致“卡车撞墙”，于是将"卡车撞墙"和"发生地震"指向"房子摇晃"，"发生地震"指向"卡车撞墙"。

于是多维随机变量的分布可以分解为：

p(x,y)=∏v∈Vp(v∣π(v)),V=图的所有结点，π(v)=v的前驱结点p(x,y)=\prod_{v \in V}p(v|\pi(v)),V=图的所有结点，\pi(v)=v的前驱结点

马尔科夫链就是有向图中的一个例子。

无向图模型：

不需要探究事情的前因后果。仅仅指向有关联的结点。

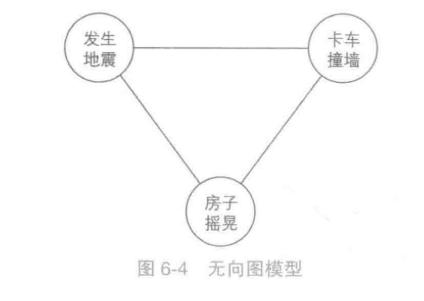
无向图将概率分解为所有最大团上的某函数的乘积。

团： 无向图的完全子图。

极大团：如果一个团不被其他任一团所包含，即它不是其他任一团的真子集，则称该团为图G的极大团

最大团：最大团就是就是结点数最多的极大团。

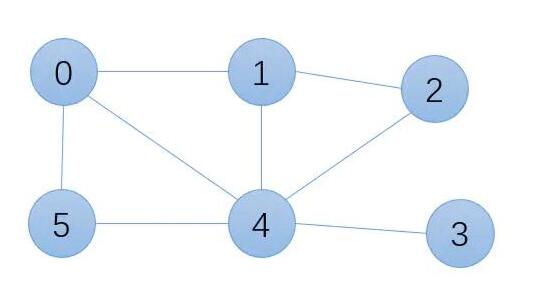
在上图中，

团有很多：{0，5}，{0，1}，{0，4，5}，{1，2，4}...

极大团：{0,4,5},{1,2,4},{0,1,4},{4,3}

最大团：{0,4,5},{1,2,4},{0,1,4}

无向图模型定义了一些虚拟的因子节点，每个因子节点只连接部分节点，组成更小的最大团

这样，该图的最大团由一个变为了4个，每个最大团变量节点变为了两个。于是，将多为随机变量的联合分布分解为了各个最大团中的因子的乘积。并且该分布为判别式模型最需要的条件概率分布。

p(y∣x)=p(x,y)=1Z∏aCa(xa,ya)a是因子节点，Ca是因子节点对应的函数，xa,ya是因子节点所有连接的变量节点Z=∑x,y∏aCa(xa,ya)（也就是归一化）p(y|x)=p(x,y)=\frac{1}{Z}\prod_{a}C_a(x_a,y_a) \\a是因子节点，C_a是因子节点对应的函数，x_a,y_a是因子节点所有连接的变量节点\\ Z=\sum_{x,y}\prod_aC_a(x_a,y_a) （也就是归一化）

在机器学习中，通常将因子函数设为：

Ca(xa,ya)=exp{∑kWakfak(xa,ya)}其中k为特征编号，fak(xa,ya)为特征函数，Wak为特征的权重C_a(x_a,y_a)=exp\{\sum_kW_{ak}f_{ak}(x_a,y_a)\}\\ 其中k为特征编号，f_{ak}(x_a,y_a)为特征函数，W_{ak}为特征的权重

条件随机场

是一种判别式模型，通过输入x，求P(y|x)。

对于HMM模型，我们是利用前一个状态转移的当前的状态，可以理解成是用前一个状态“生成”了当前的状态。

条件随机场是根据周围节点的状态来“判别”当前状态的概率。

线性链条件随机场

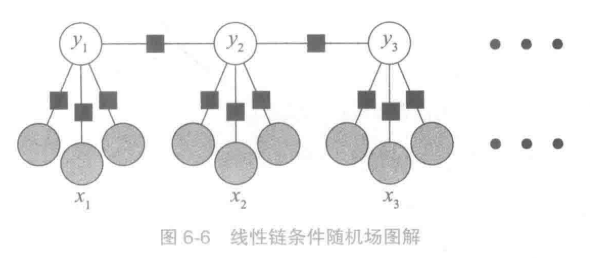
上图中，有x1，x2，x3三个变量，对应了y1，y2，y3三种状态，每个x有三个特征（灰圆球的数量）。

黑方块为因子节点也就是特征函数。将x和对应的y作为状态特征，y_{t-1}的特征作为转移特征。

于是线性链条件随机场的定义如下：

P(yt∣xt)=1Z(x)Ct(yt−1,yt,xt)=1Z(x)exp{∑k=1KWkfk(yt−1,yt,xt)}其中：Z(x)=∑yexp{∑k=1KWkfk(yt−1,yt,xt)}K为特征数，fk为特征函数，Wk为特征的权重P(y_t|x_t)=\frac{1}{Z(x)}C_t(y_{t-1},y_t,x_t)\\ =\frac{1}{Z(x)}exp\{\sum_{k=1}^KW_{k}f_{k}(y_{t-1},y_t,x_t)\}\\其中： Z(x)=\sum_{y}exp\{\sum_{k=1}^KW_{k}f_{k}(y_{t-1},y_t,x_t)\} \\K为特征数，f_{k}为特征函数，W_k为特征的权重

将该式子进行化简：

define：W={W1,W2,...,Wk}TF(yt−1,yt,xt)={f1(yt−1,yt,xt),...,fk(yt−1,yt,xt)}so:P(yt∣xt)=exp(WF(yt−1,yt,xt))Z(x)define：\\\mathbb W =\{W_1,W_2,...,W_k\}^T\\ \mathbb F(y_{t-1},y_t,x_t)=\{f_1(y_{t-1},y_t,x_t),...,f_k(y_{t-1},y_t,x_t)\}\\ so:\\ P(y_t|x_t)=\frac {exp(\mathbb W\mathbb F(y_{t-1},y_t,x_t))}{Z(x)}

CRF的三个问题

与HMM一样，CRF也存在着三个待求解的问题。在HMM中，我们将观测序列按照时刻逐个的进行计算，但是在CRF中，我们无需拆开观测序列X，相比而言，CRF更加的容易。下面我们具体描述CRF的三个基本问题：

  • 评估问题： 概率计算的问题。给定P(Y|X), 输入序列X和输出序列Y时，求P(Y_i|X)和P(Y_i,Y_{i-1}|X)的条件概率。
  • 学习问题，也就是采用训练数据X，Y训练CRF中的权重参数和条件概率。
  • 解码问题，给定CRF，条件概率分布P(Y|X)，观测序列X，求解条件概率最大的状态序列Y。

评估问题

给定相关的约束条件，即给定相关的特征函数和对应的特征函数的权重值。处理这个问题的基本算法采用前向，后向算法，其中我们定义给定的条件随机场：γ

定义：Mi(yi−1,yi∣x)=exp(∑k=1Kwkfk(yi−1,yi,x))这个式子定义了在给定yi−1时，从yi−1转移到yi的非规范化概率这样，我们很容易得到序列位置i+1的标记是yi+1时，之前的部分标记序列的非规范化概率递推公式：前向概率：αi+1(yi+1∣x)=αi(yi∣x)[Mi+1(yi+1,yi∣x)],i=1,2,...,n+1定义：α0(y0∣x)={1,y0=start0,else我们定义βi(yi∣x)表示序列位置i的标记是yi时，之后的从i+1到n的部分标记序列的非规范化概率后向概率：βi(yi∣x)=[Mi+1(yi,yi+1∣x)]βi+1(yi+1∣x),i=1,2,...,n+1定义：βn+1(yn+1∣x)={1,yn+1=stop0,else定义：M_i(y_{i−1},y_i|x)=exp(∑_{k=1}^Kw_kf_k(y_{i−1},y_i,x))\\ 这个式子定义了在给定y_{i−1}时，从y_{i−1}转移到y_i的非规范化概率\\ 这样，我们很容易得到序列位置i+1的标记是y_{i+1}时，之前的部分标记序列的非规范化概率递推公式：\\ 前向概率：α_{i+1}(y_{i+1}|x)=α_i(y_i|x)[M_{i+1}(y_{i+1},y_i|x)],i=1,2,...,n+1\\ \\ 定义：α_0(y_0|x)=\begin{cases} 1,\quad y_0=start\\ 0, \quad else \end{cases}\\ \\ 我们定义β_i(y_i|x)表示序列位置i的标记是y_i时，之后的从i+1到n的部分标记序列的非规范化概率\\ 后向概率：β_i(y_i|x)=[M_{i+1}(y_i,y_{i+1}|x)]β_{i+1}(y_{i+1}|x),i=1,2,...,n+1\\ 定义：β_{n+1}(y_{n+1}|x)=\begin{cases} 1,\quad y_{n+1}=stop\\ 0, \quad else \end{cases}\\ \\

于是我们可以计算出计算序列位置i的标记是yi时的条件概率P(Yi=yi∣x):P(Yi=yi∣x)=aiT(yi∣x)βi(yi∣x)Z(x)也能够计算序列位置i的标记是yi，位置i−1的标记是yi−1时的条件概率P(Yt−1=yt−1,Yt=yi∣x):P(Yt−1=yt−1,Yt=yi∣x)=ai−1T(yi−1∣x)Mi(yi−1,yi∣x)βi(yi∣x)Z(x)于是我们可以计算出计算序列位置i的标记是y_i时的条件概率P(Y_i=y_i|x):\\ P(Y_i=y_i|x)=\frac{{a_i}^T(y_i|x)β_i(y_i|x)}{Z(x)}\\ 也能够计算序列位置i的标记是y_i，位置i−1的标记是y_{i−1}时的条件概率P(Y_{t-1}=y_{t-1},Y_t=y_i|x):\\ P(Y_{t-1}=y_{t-1},Y_t=y_i|x)=\frac{{a_{i-1}}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x)β_i(y_{i}|x)}{Z(x)}

学习问题

我们给定训练数据集X和对应的标记序列Y，K个特征函数fk(x,y)，需要学习模型参数特征权重和条件概率Pw(y|x)，其中条件概率Pw(y|x)和模型权重wk满足以下关系

Pw(y∣x)=P(yt∣xt)=exp(∑k=1KWkfk(yt−1,yt,xt))Zw(x)P_w(y|x)=P(y_t|x_t)=\frac{exp(\sum_{k=1}^KW_{k}f_{k}(y_{t-1},y_t,x_t))}{Zw(x)}

梯度下降法求解

在使用梯度下降法求解模型参数之前，我们需要定义我们的优化函数，这里采用极大似然函数作为目标函数：

L(w)=log∏x,yPw(y∣x)P¯(x,y)=∑x,yP¯(x,y)logPw(y∣x)L(w)=log∏_{x,y}P_w(y|x)^{P^¯(x,y)}=∑_{x,y}P^¯(x,y)logP_w(y|x)

令f(w)=−log(L(W)),再对f(w)求导，则有下面的公式为：∂f(w)∂w=∑x,yP¯(x)Pw(y∣x)f(x,y)−∑x,yP¯(x,y)f(x,y)令f ( w ) = − l o g ( L ( W ) ),再对f(w)求导，则有下面的公式为： \\\frac{∂f(w)}{∂w}=∑_{x,y}P^¯(x)P_w(y|x)f(x,y)−∑_{x,y}P^¯(x,y)f(x,y)

有了w的导数表达式，就可以用梯度下降法来迭代求解最优的w了。注意在迭代过程中，每次更新w后，需要同步更新Pw(x,y),以用于下一次迭代的梯度计算。

解码问题

给定条件随机场的条件概率P(y|x)和一个观测序列x,要求出满足P(y|x)最大的序列y。

解决问题和HMM类似，采用维特比算法。

例子

假设输入的都是为三个词的句子，即 X=(X1,X2,X3) ,输出的词性记为 Y=(Y1,Y2,Y3) , 其中Y∈{1（名词），2（动词）} ，标记出取值为1的特征函数如下：

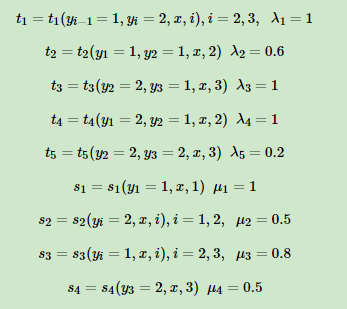
t为特征函数只和当前节点和上一个节点有关

s为特征函数只和当前节点有关

r,μ为特征权重

求观测序列（x1，x2，x2）最可能的标记序列。

解：

首先计算第一个句子词性为1，2的非规范化概率：δ1(1)=μ1s1=1δ1(2)=μ2s2=0.5首先计算第一个句子词性为1，2的非规范化概率：\\ δ_1(1)=μ1s1=1\\δ_1(2)=μ2s2=0.5

接下来进行递推，计算第二个句子：δ2(1)=max{δ1(1)+t2λ2+μ3s3,δ1(2)+t4λ4+μ3s3}=max{1+0.6+0.8,0.5+1+0.8}=2.4δ2(2)=max{δ1(2)+μ2s2,δ1(1)+t1λ1+μ2s2}=max{0.5+0.5,1+1+0.5}=2.5接下来进行递推，计算第二个句子：\\ δ_2(1)=max\{δ_1(1)+t_2λ_2+μ_3s_3,δ_1(2)+t_4λ_4+μ_3s_3\} \\=max\{1+0.6+0.8,0.5+1+0.8\}=2.4\\ δ_2(2)=max\{δ_1(2)+μ_2s_2,δ_1(1)+t_1λ_1+μ_2s_2\} \\=max\{0.5+0.5,1+1+0.5\}=2.5\\

然后计算第三个句子：δ3(1)=max{δ2(1)+μ3s3,δ2(2)+t3λ3+μ3s3}=max{2.4+0.8,2.5+1+0.8}=4.3δ3(2)=max{δ2(1)+t1λ1+μ4s4,δ2(2)+t5λ5+μ4s4}=max{2.4+1+0.5,2.5+0.2+0.5}=3.9然后计算第三个句子：\\ δ_3(1)=max\{δ_2(1)+μ_3s_3,δ_2(2)+t_3λ_3+μ_3s_3\} \\=max\{2.4+0.8,2.5+1+0.8\}=4.3\\ δ_3(2)=max\{δ_2(1)+t_1λ_1+μ_4s_4,δ_2(2)+t_5λ_5+μ_4s_4\} \\=max\{2.4+1+0.5,2.5+0.2+0.5\}=3.9\\

比较max(δ3(1),δ3(2)，得到y3=1,再逆推回去比较max(δ_3(1),δ_3(2)，得到y_3=1,再逆推回去\\

即最终的结果为(y1,y2,y1),即标记为(名词，动词，名词)。

实现

from pyhanlp import *
from pyhanlp.static import download, remove_file, HANLP_DATA_PATH
import os
import zipfile
CRFSegmenter = JClass('com.hankcs.hanlp.model.crf.CRFSegmenter')
CRFLexicalAnalyzer = JClass('com.hankcs.hanlp.model.crf.CRFLexicalAnalyzer')
CWSEvaluator = SafeJClass('com.hankcs.hanlp.seg.common.CWSEvaluator')
CRF_MODEL_PATH=None
CRF_MODEL_TXT_PATH=None
root_path=None
#创建测试数据路径
def test_data_path():
    data_path = os.path.join(HANLP_DATA_PATH, 'test')
    os.mkdir(data_path)
    CRF_MODEL_PATH = data_path + "/crf-cws-model"
    CRF_MODEL_TXT_PATH = data_path + "/crf-cws-model.txt"
    return data_path
# 下载MSR语料库
def ensure_data(data_name, data_url):
    root_path = test_data_path()
    dest_path = os.path.join(root_path, data_name)+'.zip'
    download(data_url, dest_path)
    with zipfile.ZipFile(dest_path, "r") as archive:
        archive.extractall(root_path)
    remove_file(dest_path)
    dest_path = dest_path[:-len('.zip')]
    return dest_path
sighan05 = ensure_data('icwb2-data', 'http://sighan.cs.uchicago.edu/bakeoff2005/data/icwb2-data.zip')
msr_dict = os.path.join(sighan05, 'gold', 'msr_training_words.utf8')
msr_train = os.path.join(sighan05, 'training', 'msr_training.utf8')
msr_model = os.path.join(test_data_path(), 'msr_cws')
msr_test = os.path.join(sighan05, 'testing', 'msr_test.utf8')
msr_output = os.path.join(sighan05, 'testing', 'msr_bigram_output.txt')
msr_gold = os.path.join(sighan05, 'gold', 'msr_test_gold.utf8')
## 以下开始 CRF 中文分词
def train(corpus):
    segmenter = CRFSegmenter(None)             # 创建 CRF 分词器
    segmenter.train(corpus, CRF_MODEL_PATH)
    return CRFLexicalAnalyzer(segmenter)
segment = train(msr_train)
print(CWSEvaluator.evaluate(segment, msr_test, msr_output, msr_gold, msr_dict))  # 标准化评测

由于运行过程太占时间和内存，直接使用书上的结果图

总结

CRF和HMM有很多相似之处，都包含了评估、学习、解码问题。两者都可以用于序列模型，因此都广泛用于自然语言处理的各个方面。

但是两者还是有所不同的，最大的不同点是CRF模型是判别模型，而HMM是生成模型。

属于 @威伦特 RSS