威伦特

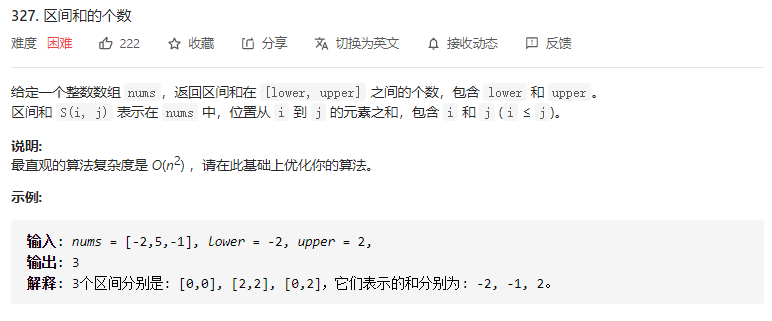
这道题首先的一个难点就是读懂题意

我首先读了几遍才明白了具体意思 意思如下：

根据例题输入：

也就是说在nums数组下标 0<=i<j<nums.size()中 寻找和区间

nums[j]+~nums[i]中 的值在lower和upper区间之间~

依此首先我们就会想到暴力法：

         int count=0;
         for(int i=0;i<nums.size();i++)
         {
             cout<<nums[i]<<" ";
             long n=0;
             for(int j=i;j<nums.size();j++)
             {
                 n+=nums[j];
             if(lower<=n&&n<=upper)  count++；
             }
          }
          return count;

但是呢，好歹这是一个困难题 哪有这么简单

很明显暴力法会超时~

于是我们可以转换思路

• 首先题目要求的是 lower<=区间[i,j]的和<=upper

• 可以转换成：lower<=sum.at(j)-sum.at(i)的和<=upper

• 通过变换:lower-sum.at(j)<=-sum.at(i)<=upper-sum.at(j)

• 去掉符号：**sum.at(j)-lower>=sum.at(i)>=sum.at(j)-upper **

• 所以最后关键东东来了 就是 sum.at(j)-upper <= sum.at(i) <= sum.at(j)-lower

• 我们于是想到了用 mutiset 自动排序的特性

• 并且mutiset 恰好有lower_bound,upper_bound这两个折半的查找函数~

• 最后通过distance来结合就可以了~

     multiset<long> helper;
     int count=0;
     helper.insert(0);
     long long sum=0;
     for (int i:nums)
     {
         sum+=i;
         count+=distance(helper.lower_bound(sum-upper),helper.upper_bound(sum-lower));
         helper.insert(sum);
     }
     return count;