威伦特

题目要求，每个皇后不能与其他皇后在同一行，同一列，同一对角线上。因此，我们可以从第一行一直往下搜索，如果符合条件，则将皇后放置在上面。

题目如下：

那么，条件应该如何设置呢？

题目分析

首先我们观察棋谱：

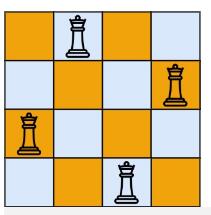
可以将上述棋谱抽象成二维数组的形式，那么每个格子对应的坐标为：

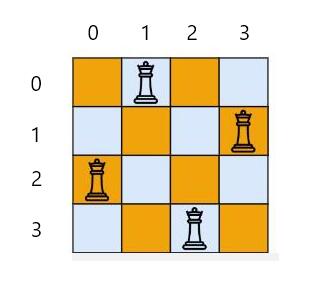
我们画一条 135°斜对角线，观察：

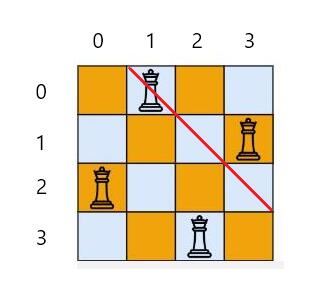
在这条对角线上的位置的下标的行列值之差， 是一个定值，为1
同时为了方便编写代码，使这样一个差值为非负数，我们加上棋盘的长度N；
那么这条对角线上是否有皇后就可以表示为：

if cdiag[n+x-y] ==True #True 表示为没有皇后

同理，画一条 45°斜对角线，观察

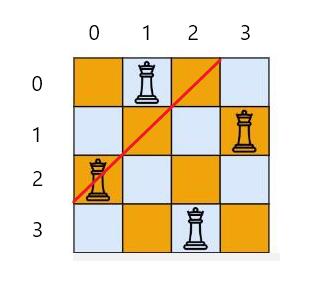
在这条对角线上的位置的下标的行列值之和， 是一个定值，为2
那么这条对角线上是否有皇后就可以表示为：

if diag[x+y] ==True #True 表示为没有皇后

所以我们判断这个位置是否应该放置皇后的时候， 只需要设立三个数组col(列), diag(正对角线), cdiag(负对角线);
然后合并判断列， 45°对角线， 135°对角线上是否有皇后即可

if(col[i]==True and diag[r+i]==True and cdiag[n+r-i]==True)  #True 表示为没有皇后

题解

有了上述分析后，现在只需要初始化棋盘，使用DFS进行遍历是否符合上述条件就可以了
首先初始化棋盘以及判断条件：

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        res=[]
        init=[['.' for i in range(n)] for i in range(n)]
        diag=[True for i in range(2*n)]
        col=[True for i in range(n)]
        cdiag=[True for i in range(2*n)]
        dfs(0,n,init,diag,col,cdiag,res)
        return res

接下来用DFS来进行遍历是否符合条件

def dfs(r,n,map,diag,col,cdiag,res):
        if(r==n):
            red=[]
            for i in map:
                red.append("".join(i))
            res.append(red)
        for i in range(0,n):
            if(col[i]==True and diag[r+i]==True and cdiag[n+r-i]==True):
                map[r][i]='Q'
                col[i]=diag[r+i]=cdiag[n+r-i]=False
                dfs(r+1,n,map,diag,col,cdiag,res)
                map[r][i] = '.'   #如果路径不对，就退回
                col[i] = cdiag[n+r-i] = diag[r+i] = True

大功告成！

拓展

在此题的基础上，我们可以消灭第52题，N皇后Ⅱ

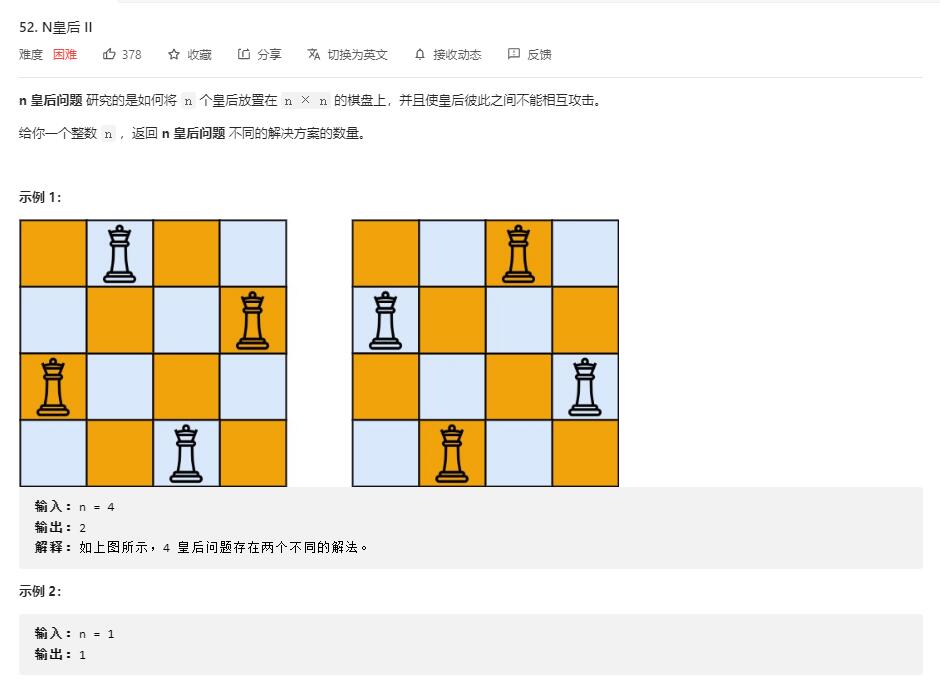
只改变一行代码，就能解决该题：

return len(res)

将返回值res改为返回res的长度即可