威伦特

今天是10.24程序员日，恰好今天的每日一题序号是1024

题解：

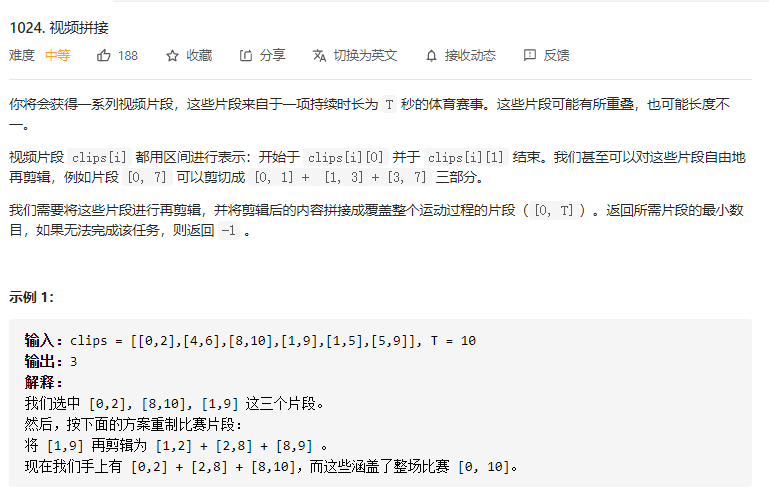
要求覆盖 [0, T] 区间的最少片段数

​

需要去获得最少的片数，我们就可以想到贪心算法了。

于是我们不妨思考：是否可以将这个片段按照开头的大小排序？

我们不妨试一试

方法一：

vector<pair<int,int>> newclips;
for(int i=0;i<row;i++) 
    newclips.push_back({clips[i][0],clips[i][1]});
sort(clips.begin(),clips.end());

构建一个pair集合数组 然后将其sort从小到大排序

方法二：

sort(clips.begin(),clips.end());

根据二维数组的性质（地址），可以直接使用sort排序

于是我们获得了一个这样的数组：

原：[[0,2],[4,6],[8,10],[1,9],[1,5],[5,9]]

新：[[0,2],[1,5],[1,9],[4,6],[5,9],[8,10]]

这样我们好像就可以使用贪心算法了

具体思路为：

左边片段不动的情况下，右边片段尽可能的要大

左边片段在移动的情况下，移动的尽可能多

依此思路可以写出如下代码：

      int right=0,i=0;
​    for(i;i<row&&right<T;)
​    {
​      int flag=0,nr=0;//flag 标志是否可以移动片段
​      while(i<row&&clips[i][0]<=right) 
​      {
​        nr=max(nr,clips[i][1]);
​        i++;flag=1;
​      }
​      count++;right=nr;
​      if(!flag) break;
​    };

当时思考的时候 使用的是

if(clips[i+1][0]>right)

发现总是有一些例子过不了，最后换了一种思考测试用例算是过了！~

所以说呢，一条路暂时走不通的时候，退回来走另一条路嘛~

最后加上判断

return r<T ? -1:cnt;

就大功告成了！