威伦特

解码生命

首页 文章 标签 关于

手写MOE

2025-09-11 10 min read # 大模型 # 代码 # NLP

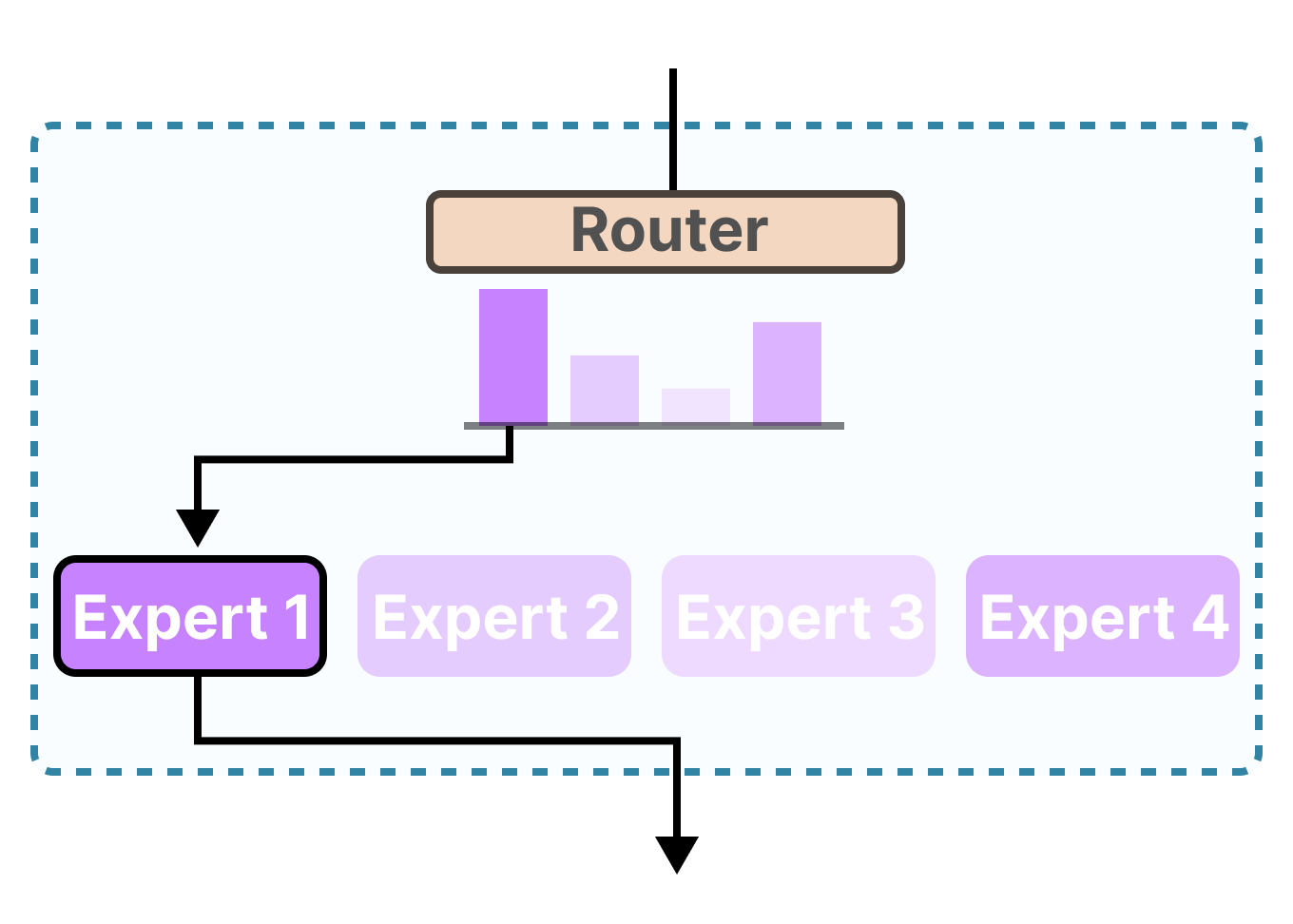
MOE（Mixture of Experts）也就是混合专家系统，已经在LLM（Large Language Model）的结构中成为标配了。最近看到一篇手写MOE教程，所学下来，受益颇多。

MOE概述

MOE的核心思想就是通过多个神经网络构成多个“领域”的专家，对输入进行一个判断，让最“擅长”这个任务的专家处理这个任务。从而实现更高效、准确的处理任务。

因此，MOE模型的必要组成部分包含：

  • 专家（Experts）：模型中的每个专家都是一个独立的神经网络，专门处理输入数据的特定子集或特定任务。通常一个Experts是一个 前馈神经网络（FeadFoward Network，FFN）

  • 门控网络（Gate Network）：门控网络的作用是决定每个输入应该由哪个专家或哪些专家来处理。通常它根据输入样本的特征计算出每个专家的权重或重要性，然后根据这些权重将输入样本分配给相应的专家。门控网络通常是一个简单的神经网络，其输出经过softmax激活函数处理，以确保所有专家的权重之和为1。

而现在 LLM + MOE 如此火热的原因主要在于：

  • 提高模型性能：通过将多个专家的预测结果进行整合，MoE模型可以在不同的数据子集或任务方面发挥每个专家的优势，从而提高整体模型的性能。在不同的任务中，激活擅长的专家，可以让模型可以更准确地对不同领域的任务进行处理。

  • 减少计算消耗：与传统的密集模型相比，MoE模型在处理每个输入样本时，只有相关的专家会被激活，而不是整个模型的所有参数都被使用。这意味着MoE模型可以在保持较高性能的同时，显著减少计算资源的消耗，特别是在LLM中，这种优势更为明显。

  • 增强模型的可扩展性：MoE模型的架构可以很容易地扩展到更多的专家和更大的模型规模。通过增加专家的数量，模型可以覆盖更广泛的数据特征和任务类型，从而在不增加计算复杂度的情况下，提升模型的表达能力和泛化能力。这种可扩展性为处理大规模、复杂的数据集提供了有效的解决方案，例如在处理多模态数据时，MoE模型可以通过设置不同的专家来专门处理不同模态的数据，实现更高效的多模态融合。

Expert

因为 MOE 网络对应着多个专家，而通常来说，专家的结构是一个前馈神经网络。

因此我们首先需要实现一个普通前馈神经网络结构的专家。

import torch
import torch.nn as nn

class MOE_basic(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super().__init__()
        self.fc = nn.Linear(in_features=input_size, out_features=hidden_size)
        self.fc2 = nn.Linear(in_features=hidden_size, out_features=output_size)
        self.active = nn.ReLU()

    def forward(self, x):
        x = self.fc2(self.active(self.fc(x)))
        return x

这个 FFN 专家先把输入向量从 input_size 维线性投影到更高的 hidden_size 维，经 ReLU激活函数， 进行非线性变换，再线性缩回 input_size 维，输出与输入同形状。

通过这种“先扩后缩”的方式能够在更高维空间中学习复杂的特征交互。

基础版本MOE

基础版本的MOE思想非常的简单，即首先将输入通过一个Gate NetWork，获得每一个专家的权重（weight），然后将输入依次通过每一个专家，最后将权重乘上专家的输出作为专家的”分析结果“，然后将每个专家的结果相加即可。

class simple_MOE(nn.Module):
    def __init__(self, input_size, hidden_size, output_size, num_experts):
        super().__init__()
        self.num_experts = num_experts
        self.experts = nn.ModuleList(
            [
                MOE_basic(input_size=input_size, hidden_size=hidden_size, output_size=output_size)
                for _ in range(num_experts)
            ]
        )
        self.gate = nn.Linear(in_features=input_size, out_features=num_experts)

    # x [batch, input_size]
    def forward(self, x):
        # shape: [batch, num_experts]
        experts_weight = self.gate(x)
        # shape: [[batch, 1, output_size] * num_experts]
        experts_out_list = [expert(x).unsqueeze(1) for expert in self.experts]
        # shape: [batch, num_experts, output_size]
        experts_out_list = torch.cat(experts_out_list, dim=1)
        # shape: [batch, 1, num_experts]
        experts_weight = experts_weight.unsqueeze(1)
        # shape: [batch, 1, output_size]
        out = experts_weight @ experts_out_list
        # shape: [batch, output_size]
        return out.squeeze(1)

Sparse MoE

Sparse MoE 开始就是大模型训练时所采用的结构了。回看基础版本的MOE，让输入进过了每一个专家的计算，然后采取了不同权重，表示对不同专家的侧重程度。但是在大模型的训练架构中，由于模型的参数量过大，这种基础版本的MOE并没有减轻训练的负担。

因此，Sparse Moe相较于基础版本的MOE的区别是，通过Router选择 topK 个专家，然后对这 topK 个专家的输出进行加权求和。

如果 topK = 专家数量，那么其实也退化成了基础版本的MOE

具体结构如下图所示：

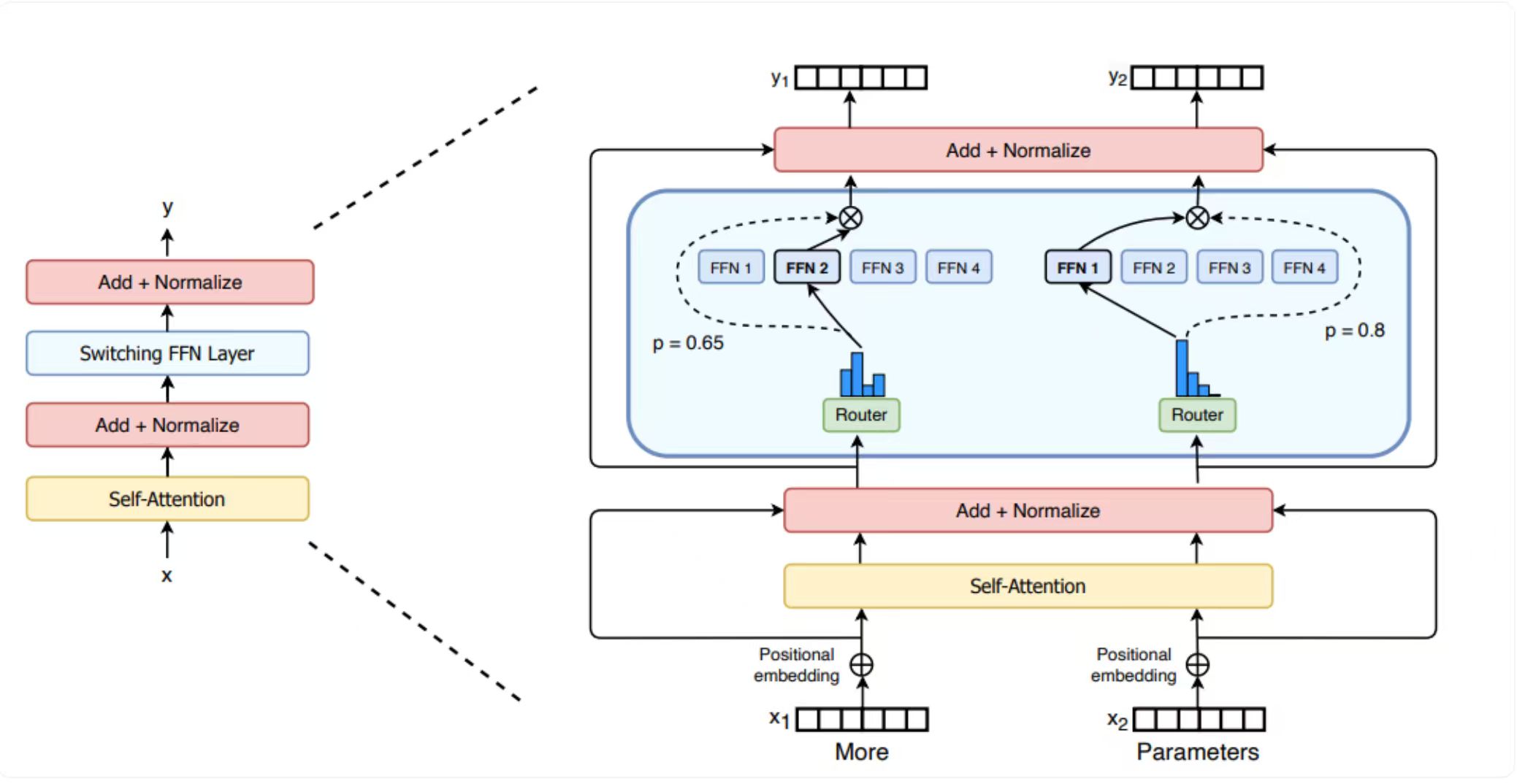
以 switch transformers 模型的 MOE 架构图作为演示

首先是 Router，对每个 token 通过 top-k 选择专家

class MOE_router(nn.Module):
    def __init__(self, hidden_size, num_experts, top_k):
        super().__init__()
        self.num_experts = num_experts
        self.gate = nn.Linear(in_features=hidden_size, out_features=num_experts)
        self.top_k = top_k

    # hidden_states :[batch* seq, hidden_size]
    def forward(self, hidden_states):
        routers_logits = self.gate(hidden_states)  # shape: [batch* seq, num_experts]
        routers_probs = F.softmax(
            routers_logits, dim=-1, dtype=torch.float
        )  # shape:[batch* seq, num_experts]
        router_weights, selected_experts = torch.topk(
            routers_probs, self.top_k, dim=1
        )  # shape:[batch* seq,top_k], topk 返回选择的top-k的值和对应的索引
        router_weights = router_weights / router_weights.sum(
            dim=-1, keepdim=True
        )  # 归一化
        router_weights = router_weights.to(hidden_states.dtype)  # 转换精度
        # 生成专家掩码，提升计算效率
        experts_mask = F.one_hot(
            selected_experts, num_classes=self.num_experts
        )  # 选的是1，没选的是0 shape:[batch* seq, top_k, num_experts]
        experts_mask = experts_mask.permute(2, 1, 0)  # (num_experts, top_k, batch* seq)
        return routers_logits, router_weights, selected_experts, experts_mask

class spare_MOE(nn.Module):
    def __init__(self, input_size, output_size, hidden_size, top_k, num_experts):
        super().__init__()
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size = hidden_size
        self.num_experts = num_experts
        self.top_k = top_k
        self.router = MOE_router(self.hidden_size, num_experts, top_k)
        self.MOE = nn.ModuleList([MOE_basic(input_size, output_size) for _ in range(num_experts)])

    def forward(self, x):
        # x shape [batch, seq,hidden_size]
        print(x.shape)
        batch_size, seq, hidden_size = x.size()
        # 合并强两个维度，将所有token视为独立的输入，这样每个专家可以独立处理每个token，而不需要考虑它们属于哪个批次或序列
        # [batch*seq, hidden_size]
        hidden_state = x.view(-1, hidden_size)
        routers_logits, router_weights, selected_experts, experts_mask = self.router(hidden_state)
        print(routers_logits.shape, router_weights.shape, selected_experts.shape, experts_mask.shape)
        final_hidden_states = torch.zeros_like(hidden_state)
        for experts_idx in range(self.num_experts):
            experts_layer = self.MOE[experts_idx]  # 当前专家网络
            # idx [top_k]
            # top_X [batch* seq]
            idx, top_x = torch.where(experts_mask[experts_idx] == 1)
            # 选出哪些token需要经过专家
            current_state = hidden_state.unsqueeze(0)[:, top_x, :].reshape(-1, hidden_size)
            # 专家处理*权重
            current_hidden_state = experts_layer(current_state) * router_weights[top_x, idx].unsqueeze(-1)
            final_hidden_states.index_add(0, top_x, current_hidden_state.to(hidden_state.dtype))
        final_hidden_states = final_hidden_states.reshape(batch_size, seq, hidden_size)
        return final_hidden_states, routers_logits

然后是整个 Sparse MoE 的代码

class spare_MOE(nn.Module):
    def __init__(self, input_size, output_size, hidden_size, top_k, num_experts):
        super().__init__()
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size = hidden_size
        self.num_experts = num_experts
        self.top_k = top_k
        self.router = MOE_router(self.hidden_size, num_experts, top_k)
        self.MOE = nn.ModuleList([MOE_basic(input_size, hidden_size, output_size) for _ in range(num_experts)])

    def forward(self, x):
        # x shape [batch, seq,hidden_size]
        print(x.shape)
        batch_size, seq, hidden_size = x.size()
        # 合并强两个维度，将所有token视为独立的输入，这样每个专家可以独立处理每个token，而不需要考虑它们属于哪个批次或序列
        # [batch*seq, hidden_size]
        hidden_state = x.view(-1, hidden_size)
        routers_logits, router_weights, selected_experts, experts_mask = self.router(hidden_state)
        print(routers_logits.shape, router_weights.shape, selected_experts.shape, experts_mask.shape)
        final_hidden_states = torch.zeros_like(hidden_state)
        for experts_idx in range(self.num_experts):
            experts_layer = self.MOE[experts_idx]  # 当前专家网络
            # idx [top_k]
            # top_X [batch* seq]
            idx, top_x = torch.where(experts_mask[experts_idx] == 1)
            # 选出哪些token需要经过专家
            current_state = hidden_state.unsqueeze(0)[:, top_x, :].reshape(-1, hidden_size)
            # 专家处理*权重
            current_hidden_state = experts_layer(current_state) * router_weights[top_x, idx].unsqueeze(-1)
            final_hidden_states.index_add(0, top_x, current_hidden_state.to(hidden_state.dtype))
        final_hidden_states = final_hidden_states.reshape(batch_size, seq, hidden_size)
        return final_hidden_states, routers_logits

ShareExpert Sparse MoE

ShareExpert SparseMoE 则是 Deepseek 所采用的一种 MOE架构。

和上面的 Sparse MoE 的区别是，ShareExpert Sparse MoE 增加了一组共享的专家模型。这些模型是所有输入的 token 共享的，也就是说，所有 token 都过这些共享专家模型，然后每个 token 再经过Sparse Moe，选出 top-k 个专家，然后这 top-K 个专家和共享的专家的输出一起再加权求和。

具体结构如下图所示：

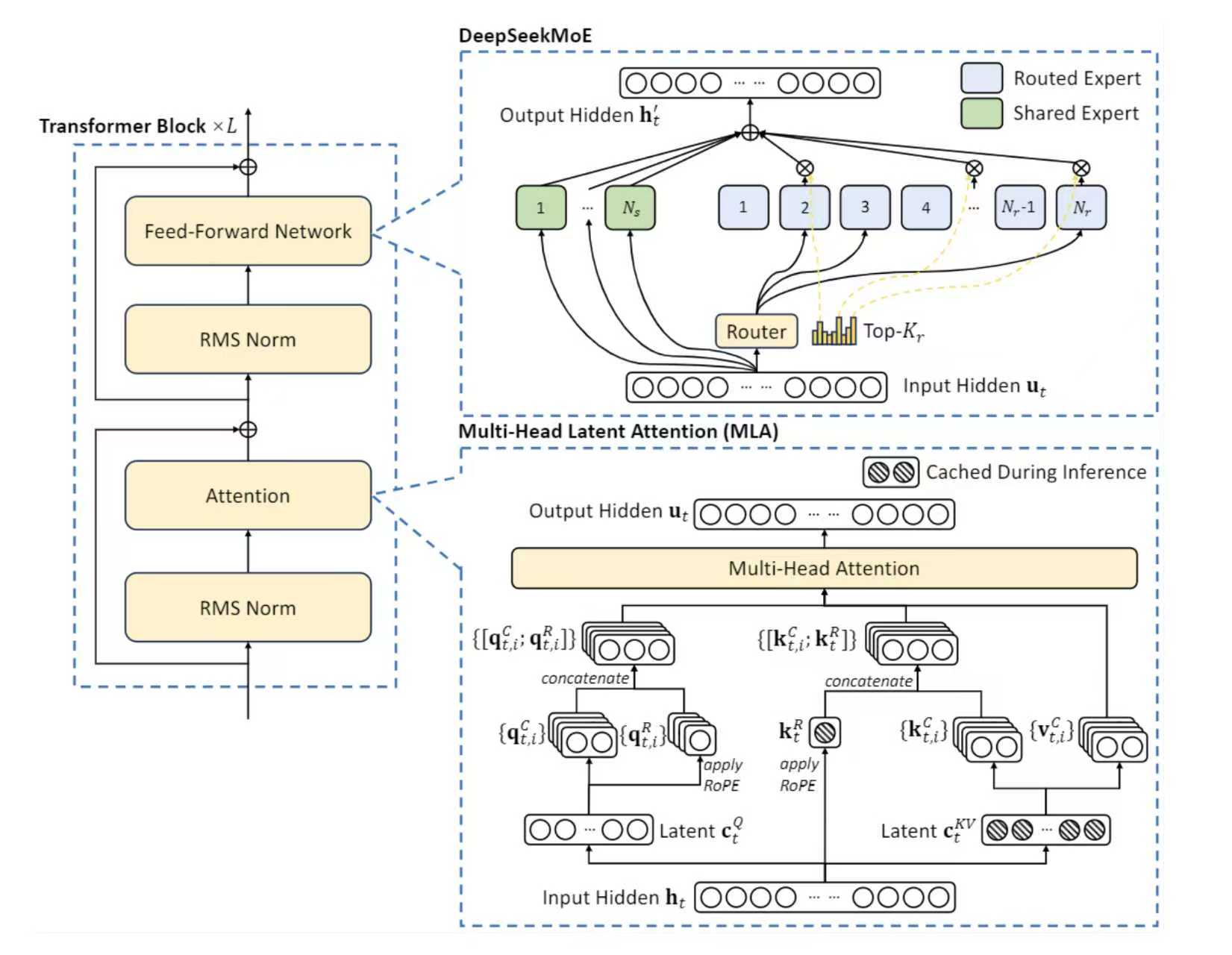
下面的手写代码参考了 deepseek MoE 的思想，有一定的简化，但是可以方便理解训练过程。

class shareExpert_MOE(nn.Module):
    def __init__(self, input_size, output_size, hidden_size, top_k, num_experts):
        super().__init__()
        self.spare_MOE = spare_MOE(input_size, output_size, hidden_size, top_k, num_experts)
        self.share_MOE = nn.ModuleList(
            [MOE_basic(input_size=input_size, hidden_size=hidden_size, output_size=output_size) for _ in range(num_experts)]
        )

    def forward(self, x):
        # spare_moe_out [batch, seq, hidden], routers_logits [batch* seq, num_experts]
        spare_moe_out, routers_logits = self.spare_MOE(x)
        share_moe_out = [
            expert(x) for expert in self.share_MOE
        ]  # [batch, seq, hidden]
        share_moe_out = torch.stack(share_moe_out, dim=0).sum(dim=0)
        return share_moe_out + spare_moe_out, routers_logits

参考文章

LLM MOE的进化之路，从普通简化 MOE，到 sparse moe，再到 deepseek 使用的 share_expert sparse moe | chaofa用代码打点酱油

属于 @威伦特 RSS