威伦特

最近学习神经网络的时候，发现大多介绍神经网络的文章都是先大篇幅的描述概念，然后莫名其妙就丢出很多晦涩难懂的数学公式，就结束了，让人看得一头雾水。
直到最近看了一篇文章，它通过实例和概念相结合的方式介绍神经网络，对初学者十分友好，于是我将其与其他文章整合，加上自己的理解，写出这篇文章。

什么是神经网络

简单介绍一下神经网络，

以房价预测的来说明，把房屋的面积作为神经网络的输入（我们称之为𝑥），通过一个节点（一个小圆圈），最终输出了价格（我们用𝑦表示），那么这个节点就是神经元，而无数个神经元就组成了神经网络

神经网络的一般结构是由输入层、隐藏层(神经元)、输出层构成的。隐藏层可以是1层或者多层叠加，层与层之间是相互连接的，如下图所示。

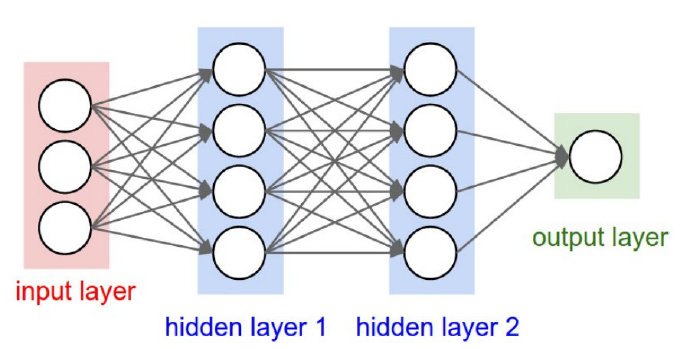
一般说到神经网络的层数是这样计算的，输入层不算，从隐藏层开始一直到输出层，一共有几层就代表着这是一个几层的神经网络，例如上图就是一个三层结构的神经网络。

已经知道了神经网络的概念，接下来开始尝试一下通过代码来理解和实现一个神经网络吧！

构建神经元

“千里之行，始于足下”，我们先从一个神经元开始构建。

神经元接受输入，做一些数学运算，然后产生一个输出。下图是一个2输入神经元

神经元中，输入的数据总共经历了三步数学运算。

首先将输入乘上权重：

$x_1 \rightarrow x_1∗w_1\\ x_2 \rightarrow x_2*w_2$

接下来将结果相加，再加上一个偏移值(bias):

$(x_1*w_1)+(x_2*w_2)+b$

最后，将结果放入激活函数中(activation function):

$y=f(x_1*w_1+x_2*w_2+b)$

那么，什么是激活函数呢？

激活函数的作用就是将输入转化为可预测的输出，常用的激活函数是sigmoid函数

$S(x)=\frac{1}{1+e^{-x}}$

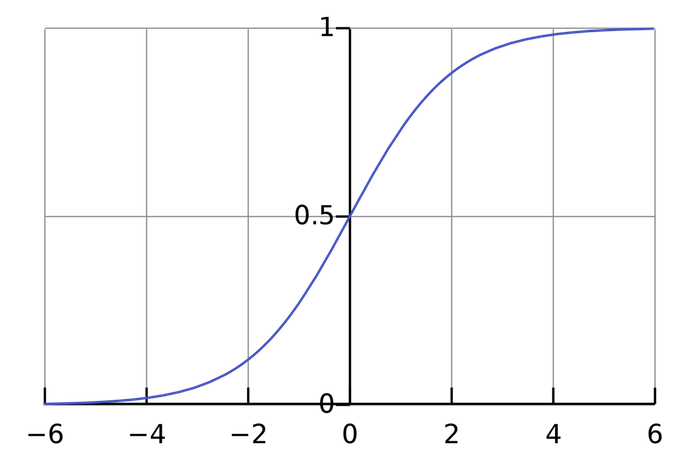
sigmoid函数的输出介于0~1之间，可以理解为sigmoid将(−∞,+∞) 的数压缩到了(0, 1)这个区间。

当然还有其他的激活函数：

• tanh(双曲正切)函数：$\ g(z)=\frac{e^z−e^{−z}}{e^z+e^{−z}},g(z)'=1−(tanh(z))^2$

• ReLu(修正线性单元)函数: 只要𝑧是正值的情况下，导数恒等于 1，当𝑧是负值的时候，导数恒等于 0。$\ a=max(0,z)$

激活函数优缺点：

• 在𝑧的区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于0，在程序实现就是一个 if-else 语句，而 sigmoid 函数需要进行浮点四则运算，在实践中，使用 ReLu 激活函数神经网络通常会比使用 sigmoid 或者 tanh 激活函数学习的更快。
• sigmoid 和 tanh 函数的导数在正负饱和区的梯度都会接近于 0，这会造成梯度弥散，而 Relu 和 Leaky ReLu 函数大于 0 部分都为常数，不会产生梯度弥散现象。(同时应该注意到的是，Relu 进入负半区的时候，梯度为 0，神经元此时不会训练，产生所谓的稀疏性，而 Leaky ReLu 不会有这问题) 𝑧在 ReLu 的梯度一半都是 0，但是，有足够的隐藏层使得 z 值大于 0，所以对大多数的训练数据来说学习过程仍然可以很快。

---

本文以sigmoid函数作为激活函数

举个例子

在上图的神经元中，输入有两个参数，我们假设神经元中参数为：

$weight=[0,1]\\ bias=4$

如果我们输入的参数$\ x_1，x_2$分别为2，3，那么经过神经元的运算后，输出的值为：

$(w⋅x)+b\\=((x_1*w_1)+(x_2*w_2))+b\\ =0*2+1*3+4\\ =7\\ Then\ put\ in \ activation\ function: \\output=f((w⋅x)+b)\\ =0.999$

这样向前传递输入以获得输出的过程被称为正向传播。

实现代码

def sigmoid(x):
    return 1 / (1 + np.exp(-x))


class Neuron:
    def __init__(self, weights, bias):
        self.weights = weights
        self.bias = bias

    def feedforward(self, inputs):
        return sigmoid(np.dot(self.weights, inputs) + self.bias)
    
    
if __name__ == '__main__':
    n = Neuron([0, 1],4)
    print(n.feedforward([2,3]))

0.9990889488055994

将神经元组合成神经网络

我们已经知道，神经网络实际上是由多个神经元组成的，下图是一个简单的神经网络

这个神经网络有2个输入值$\ x_1,x_2$，隐藏层中有两个神经元$\ h_1,h_2$，输出层有一个神经元$\ o_1$

举个例子

简单的假设每个神经元有相同的权重和偏移值,有着相同的激活函数

$weight=[0,1],\ bias=0\\ S(x)=\frac{1}{1+e^{-x}}$

如果输入的值为x=[2,3]，那么我们可以计算出神经网络中$\ h_1,h_2,o_1$所代表的值

$h_1=h_2=f(w⋅x+b)\\ =f((0*2+1*3)+0) \\=f(3) \\=0.9526 \\ o_1=f(w⋅[h_1,h_2]+b) \\=f((0∗h_1)+(1∗h_2)+0 \\=f(0.9526) \\=0.7216$

因此在这个神经网络中，在输入x=[2,3]时，输出为0.7216

---

神经网络可以有任意数量的层，在这些层中有任意数量的神经元。

但是其基本的思想是一样的:通过网络中的神经元向前输入，最终得到输出。

实现代码

import numpy as np


class Neuron:
    def __init__(self, weights, bias):
        self.weights = weights
        self.bias = bias

    def feedforward(self, inputs):
        return sigmoid(np.dot(self.weights, inputs) + self.bias)
    
    
class OurNeuralNetwork:
  def __init__(self):
    weights = np.array([0, 1])
    bias = 0
    self.h1 = Neuron(weights, bias)
    self.h2 = Neuron(weights, bias)
    self.o1 = Neuron(weights, bias)

  def feedforward(self, x):
    out_h1 = self.h1.feedforward(x)
    out_h2 = self.h2.feedforward(x)
    out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
    return out_o1


if __name__ == "__main__":
    network = OurNeuralNetwork()
    x = np.array([2, 3])
    print(network.feedforward(x))

0.7216

训练神经网络

我们有如下数据集：

Name	Weight	Height	Gender
Alice	54.5	165	女
Bob	66	170	男
Charlie	48	158	女
Diana	65	171	女
Jack	70.5	181.3	男
Loony	58	172	男

接下来让我们通过数据集来训练神经网络，使其能通过给定身高体重来预测一个人的性别吧！

第一步

我们首先通过0和1来分别代表女性和男性，同时为了能够方便表示数据，我们将身高和体重分别减去170和60

Name	Weight	Height	Gender
Alice	-5.5	-5	1
Bob	6	0	0
Charlie	-12	-12	1
Diana	5	1	1
Jack	10.5	11.3	0
Loony	-2	2	0

在训练神经网络之前，我们首先需要有一种能知道神经网络中输出值是否表现得“好”与“坏”的方法，这种方法就称作 "损失函数"

常用的损失函数为MSE（mean squared error），也就是均方差

$MSE=\frac{1}{n}\sum_{i=1}^{n}(y_{true}-y_{pred})^2$

其中，n代表训练样本的数量，$\ y_{true}$代表训练样本中的真实值，$\ y_{pred}$代表神经网络中输出的预测值

换句话说：

训练神经网络=尝试寻找损失函数最小值

举个例子

Name	$\ y_{true}$	$\ y_{pred}$	$\ (y_{true} - y_{pred})^2$
Alice	1	0	1
Bob	0	0	0
Charlie	1	0	1
Diana	1	0	1
Jack	0	0	0
Loony	0	0	0

$MSE=\frac{1}{6}(1+0+1+1+0+0) \\=0.5$

实现代码

def lossFunction(yT, yF):
    res = 0
    for (i, j) in zip(yT, yF):
        res += (i - j) ** 2
    return res / len(yT)
yT=[1,0,1,1,0,0]
yF=[0,0,0,0,0,0]
print(lossFunction(yT,yF))

0.5

第二步

我们现在有了一个清晰的目标——寻找损失函数的最小值，同时我们知道可以通过改变神经网络中的权重和偏移值来改变神经网络的输出值，那么我们怎样才能通过改变权重和偏移值来降低损失函数的值呢？

下面我们通过Alice的样本来进行说明

Name	Weight	Height	Gender
Alice	-5.5	-5	1

Alice样本的损失函数如下：

$L=MSE=\frac{1}{1}\sum_{i=1}^1(y_{true}-y_{pred})^2 \\=(1-y_{pred})^2$

接下来，我们探究一下权重和偏移值对损失函数的具体影响：

我们可以把损失函数写成一个多变量函数

$L(w_1,w_2,w_3,w_4,w_5,w_6,b_1,b_2,b_3)$

如果调整一下$\ w_1$，损失函数是会变大还是变小？我们需要知道偏导数$\ \frac{∂L}{∂w_1}$是正是负才能回答这个问题。

首先，根据链式求导法则

$\frac{∂L}{∂w_1}= \frac{∂L}{∂y_{pred}}*\frac{∂y_{pred}}{∂w_1}$

由于$\ L=(1-y_{pred})^2$,因此:

$\frac{\partial L}{\partial y_{pred}} =\frac{\partial(1-y_{pred})^2}{\partial y_{pred}}=-2(1-y_{pred})……①$

接下来我们要想办法获得$\ y_{pred}$和$\ w_1$的关系，我们已经知道神经元$\ h_1、h_2和o_1$的数学运算规则：

$y_{pred}=o_1=f(w_5h_1+w_6h_2+b_3)$

实际上只有神经元$\ h_1$中包含权重$\ w_1$，所以我们再次运用链式求导法则：

$\frac{∂y_{pred}}{∂w_1}=\frac{∂y_{pred}}{∂h_1}*\frac{∂h_1}{∂w_1}$

同理：

$\frac{∂y_{pred}}{h_1}=w_5*f′(w_5h_1+w_6h_2+b_3)……② \\h_1=f(w_1x_1+w_2x_2+b_1) \\ \frac{∂h_1}{∂w_1}=x_1*f′(w_1x_1+w_2x_2+b_1)……③$

我们在上面的计算中遇到了2次激活函数sigmoid的导数f′(x)，sigmoid函数的导数很容易求得：

$f(x)= \frac{1}{1+e^{-x}} \\ f'(x)=\frac{e^{-x}}{(1+e^{-x})^2}=f(x)*(1-f(x))$

总的链式求导公式为①②③

$\frac{∂L}{∂w_1}= \frac{∂L}{∂y_{pred}}*\frac{∂y_{pred}}{∂h_1}*\frac{∂h_1}{∂w_1}$

这种通过求偏导而从后向前进行计算的，我们称为反向传播

---

Name	Weight	Height	Gender
Alice	-5.5	-5	1

接下来我们通过Alice样本，并假设所有权重为1，所有偏移值为0，带入来计算一下神经网络中的各个数值

$h_1=f(w_1x_1+w_2x_2+b_1) \\=f(-5.5+-5+0)\\ =0.0000275 \\ h2=f(w_3x_1+w_4x_2+b_2)=0.0000275 \\ o_1=f(w_5h_1+w_6h_2+b_3)\\ =f(0.0000275+0.0000275+0) \\=0.50$

神经网络的输出$\ y_{pred}=0.5$，没有显示出强烈的是女（1）是男（0）的证据。现在的预测效果还很不好。

我们再计算一下当前网络的偏导数$\ \frac{∂L}{∂w1}$：

$\frac{∂L}{∂w_1}= \frac{∂L}{∂y_{pred}}*\frac{∂y_{pred}}{∂h_1}*\frac{∂h_1}{∂w_1} \\ \frac{\partial L}{\partial y_{pred}} =-2(1-y_{pred})\\ =-2(1-0.5)\\=-1\\ \frac{∂y_{pred}}{h_1}=w_5*f′(w_5h_1+w_6h_2+b_3)\\ =1*f'(0.0000275+0.0000275+0)\\ =f(0.000055)*(1-f(0.000055)) \\=0.250 \\ \frac{∂h_1}{∂w_1}=x_1*f′(w_1x_1+w_2x_2+b_1)\\ =-5.5*f'(-10.5) \\=-0.00015 \\ \frac{∂L}{∂w_1}=-1*0.25*-0.00015\\ =0.0000375$

由此得出，当我们增加$\ w_1,L$ 也会略微的增加。

第三步

下面将使用一种称为随机梯度下降（SGD）的优化算法，来训练神经网络的参数。

经过前面的运算，我们已经有了训练神经网络所有数据。但是该如何操作呢？

SGD定义了改变权重和偏置的方法：

$w=w-n\frac{∂L}{∂w_1}$

其中$\ n$是一个常数，称为学习率（learning rate），它决定了我们训练网络速率的快慢。将w减去$\ η·\frac{∂L}{∂w1}$，就等到了新的权重w。

• If$\ \frac{\partial L}{\partial w_1}$是正数，那么w就会减少,这将会使损失函数L降低.

• If$\ \frac{\partial L}{\partial w_1}$是负数，那么w就会增加,这将会使损失函数L降低.

如果我们用这种方法去逐步改变网络的权重w和偏置b，损失函数会缓慢地降低，从而改进我们的神经网络。

训练流程如下：

1、从数据集中选择一个样本；
2、计算损失函数对所有权重和偏置的偏导数；
3、使用更新公式更新每个权重和偏置；
4、回到第1步。

我们用Python代码实现这个过程：

Name	Weight	Height	Gender
Alice	-5.5	-5	1
Bob	6	0	0
Charlie	-12	-12	1
Diana	5	1	1
Jack	10.5	11.3	0
Loony	-2	2	0

import numpy as np


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def diff_sigmoid(x):
    fx = sigmoid(x)
    return fx * (1 - fx)


def lossFunction(yT, yF):
    res = 0
    for (i, j) in zip(yT, yF):
        res += (i - j) ** 2
    return res / len(yT)


class Neuron:
    def __init__(self, weights, bias):
        self.weights = weights
        self.bias = bias

    def feedforward(self, inputs):
        total = np.dot(self.weights, inputs) + self.bias
        return sigmoid(total)


class NeuronNetworks:
    def __init__(self, weight, bias):
        self.w1 = weight[0]
        self.w2 = weight[1]
        self.w3 = weight[2]
        self.w4 = weight[3]
        self.w5 = weight[4]
        self.w6 = weight[5]
        self.b1 = bias[0]
        self.b2 = bias[1]
        self.b3 = bias[2]

    def calculation(self, x):
        h1 = sigmoid(self.w1 * float(x[1]) + self.w2 * float(x[2]) + self.b1)
        h2 = sigmoid(self.w3 * float(x[1]) + self.w4 * float(x[2]) + self.b2)
        o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
        return o1

    def train(self, dataSets):
        n = 0.1
        y_T = [int(i[3]) for i in dataSets]
        for epoch in range(15000):
            for x,y_true in zip(dataSets,y_T):
                sum_h1=float(x[1]) * self.w1 + int(x[2]) * self.w2 + self.b1
                sum_h2=float(x[1]) * self.w1 + int(x[2]) * self.w2 + self.b1
                h1 = sigmoid(float(x[1]) * self.w1 + float(x[2]) * self.w2 + self.b1)
                h2 = sigmoid(float(x[1]) * self.w3 + float(x[2]) * self.w4 + self.b2)
                pre = h1 * self.w5 + h2 * self.w6 + self.b3
                y_pre = sigmoid(h1 * self.w5 + h2 * self.w6 + self.b3)
                Diff_output_Diff_pre = -2 * (y_true - y_pre)
                Diff_pre_Diff_h1 = self.w5 * diff_sigmoid(pre)
                Diff_pre_Diff_h2 = self.w6 * diff_sigmoid(pre)
                Diff_pre_Diff_w5 = h1 * diff_sigmoid(pre)
                Diff_pre_Diff_w6 = h2 * diff_sigmoid(pre)
                Diff_pre_Diff_b3 = diff_sigmoid(pre)
                Diff_h1_Diff_w1 = float(x[1]) * diff_sigmoid(sum_h1)
                Diff_h1_Diff_w2 = float(x[2]) * diff_sigmoid(sum_h1)
                Diff_h2_Diff_w3 = float(x[1]) * diff_sigmoid(sum_h2)
                Diff_h2_Diff_w4 = float(x[2]) * diff_sigmoid(sum_h2)
                Diff_h1_Diff_b1 = diff_sigmoid(sum_h1)
                Diff_h2_Diff_b2 = diff_sigmoid(sum_h2)
                self.w1 -= n * Diff_output_Diff_pre * Diff_pre_Diff_h1 * Diff_h1_Diff_w1
                self.w2 -= n * Diff_output_Diff_pre * Diff_pre_Diff_h1 * Diff_h1_Diff_w2
                self.w3 -= n * Diff_output_Diff_pre * Diff_pre_Diff_h2 * Diff_h2_Diff_w3
                self.w4 -= n * Diff_output_Diff_pre * Diff_pre_Diff_h2 * Diff_h2_Diff_w4
                self.w5 -= n * Diff_output_Diff_pre * Diff_pre_Diff_w5
                self.w6 -= n * Diff_output_Diff_pre * Diff_pre_Diff_w6
                self.b1 -= n * Diff_output_Diff_pre * Diff_pre_Diff_h1 * Diff_h1_Diff_b1
                self.b2 -= n * Diff_output_Diff_pre * Diff_pre_Diff_h2 * Diff_h2_Diff_b2
                self.b3 -= n * Diff_output_Diff_pre * Diff_pre_Diff_b3
            if epoch % 10 == 0:
                y_pre = []
                for x in dataSets:
                    y_pre.append(self.calculation(x))
                print(f"Epoch is {epoch} and loss is:{lossFunction(y_T, y_pre)}")


DataSet = [
    ['Alice', 54.5, 165, 1],
    ['bob', 66, 170, 0],
    ['charlie', 48, 158, 1],
    ['diana', 65, 171, 1],
    ['jack', 70.5, 181.3, 0],
    ['loony', 58, 172, 0]
]
if __name__ == '__main__':
    weights = np.array(
        [np.random.normal(), np.random.normal(), np.random.normal(), np.random.normal(), np.random.normal(),
         np.random.normal()])
    bias = [np.random.normal(), np.random.normal(), np.random.normal()]
    nn = NeuronNetworks(weights, bias)
    for i in range(len(DataSet)):
        DataSet[i][1]-=60
        DataSet[i][2]-=170
    nn.train(DataSet)

随着迭代次数的增加，损失函数逐步减少最终趋向稳定

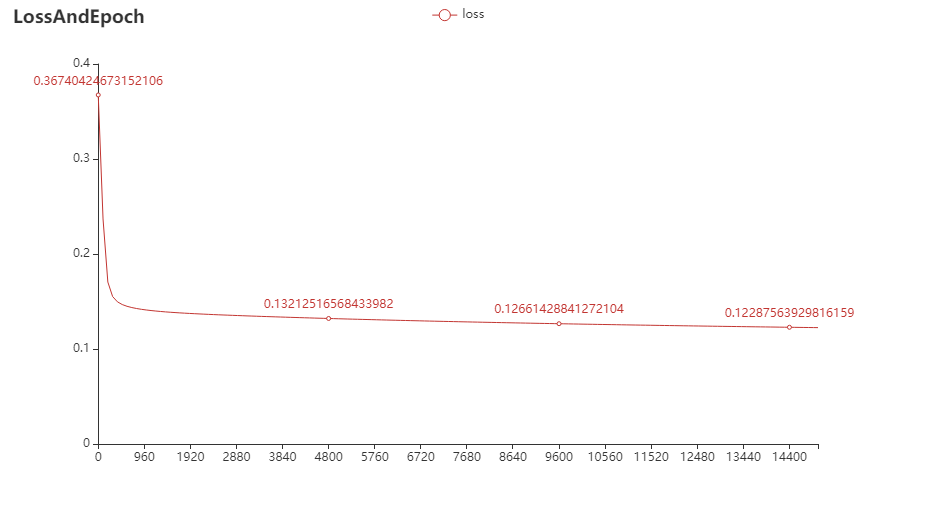
现在我们可以用它来推测出每个人的性别了：

    print(round(nn.calculation(['anna',51-60, 157-170])))  #1->女性
    print(round(nn.calculation(['bamba',75-60, 178-170]))) #0->男性

参考文章

• Machine Learning for Beginners: An Introduction to Neural Networks
• 【深度学习】神经网络