RoPE（旋转位置编码）是一种结合了绝对位置编码和相对位置编码的一种编码方法，出自苏剑林老师提出的RoFormer，现如今已经作为LLM结构的标配了，可见其效果强大。这篇文章就来具体解析一下，RoPE的原理和优势到底是什么。

本文对RoPE的解析主要参考自苏剑林老师本人对RoPE的解析系列文章^[1,2]，并结合了个人对其的一些思考。

位置编码

大模型通过理解用户的输入而进行输出。在大模型的整个理解过程中，而对句子的理解来说，字词表示和位置的准确性表示无疑非常重要，本文所探讨的就是对位置的准确性表示。

对输入的自然语言来说，由一组相同字词组成的句子，字词在句子中出现的顺序不同，都可能会导致句子所表达的含义出现偏差，简单举个例子：

用户层面

用户输入：

我 爱 你

如果对位置的准确性无法进行准确区分，模型可能会理解成：

你 爱 我

完全偏离了用户输入的意思。

给定token 序列 $[x_1, x_2, x_3]$，模型编码成对应的词向量$[e_1, e_2, e_3]$，向量开始为随机初始化，具有轮换对称性，即：$[x_1, x_2, x_3] = [x_3, x_2, x_1]$，这就会使得模型无法从结果上区分输入是$[x,y]$还是$[y,x]$，导致出现理解的偏差。

因此，我们要做的事情，就是要打破这种对称性，比如在每个位置上都加上一个不同的编码向量：$f(x_1+p_1,x_2+p_2,...)=[x_1+p_1,x_2+p_2,...]$，只要每个位置的编码向量不同，那么这种对称性就被打破了。

下面进一步分析位置编码的性质。

为了简化问题，我们先只考虑$m,n$两个位置上的位置编码，将其泰勒展开到二阶：

$f(m+p_m,n+p_n)=f(m,n)+ \frac{\partial f}{\partial m}p_m+\frac{\partial f}{\partial n}p_n + \frac{1}{2}\frac{\partial^2 f}{\partial m^2}p_m +\frac{1}{2}\frac{\partial^2 f}{\partial n^2}p_m + \frac{\partial^2 f}{\partial m \partial n}p_m.p_n$

可以看到，展开式中$f(m,n)$与位置无关，$\frac{\partial^2 f}{\partial m \partial n}p_m.p_n$ 是一个包含$m$和$n$位置信息的交互项，其余的各项都依赖于单一的位置信息。 这样就能去区分token之间的位置信息了。

针对token位置的准确性表示，主要有两个方向的研究，即相对位置编码和绝对位置编码。

绝对位置编码

绝对位置嵌入类似于为每个位置分配唯一编号，在标准的Transformer架构即使用的绝对位置编码，第一层属于除了InputEmbedding之外，还有一个同维度的PositionalEmbedding，如下所示。

$\left\{ \begin{array}{lr} PE(pos,2i) = sin(\frac{pos}{10000^{2i/d}}) \\ PE(pos,2i+1) = cos(\frac{pos}{10000^{2i/d}}) \end{array} \right.$

其中$pos$为输入的token在序列中的实际位置（0,1,2...,n-1），$d$是向量维度，$i$用于区分向量维度中的奇数位和偶数位置。然后将PositionalEmbedding与token嵌入相加，再输入Transformer。

尽管绝对位置编码实现简单，可预先计算好，不用参与训练，速度快，但也存在一些局限性。

绝对位置编码的局限性

1. 对未见过序列长度的外推：Transformer中定义的固定正弦编码，理论上可以为任何位置生成编码。尽管在数学上已定义，但是模型本身可能没有学会在其训练分布之外很远距离或绝对位置上有效理解位置信息。正弦模式在非常大的位置上可能会变得不那么清晰或可能出现混叠，使得模型难以准确区分远距离的词元

2. 固定编码的不灵活性：尽管正弦编码提供数学外推能力，但它们固定的性质意味着它们不适应训练数据或下游任务的特定特征。正弦形式对位置关系施加了特定的结构，这可能并非总是最佳的。学习得到的嵌入通过在训练期间进行适应提供更大的灵活性，但如前所述，它们在泛化到更长序列方面表现不佳。固定编码的外推能力与学习嵌入的适应性之间的这种权衡，突显了绝对位置方法的一个核心局限性。

相对位置编码

在句子"I am a student"中，“I”的实际距离是1，“Student”的实际距离是4，这是token 间的绝对距离。相对位置嵌入是这样考量的，"I"与"student"的相对距离为3，与"am"的相对距离为1。

相对位置编码的核心思想是修改注意力机制或其输入，通过相对位置差影响标记i和标记j之间的注意力得分，将查询和键位置之间的偏移信息直接注入到它们的交互计算里。

因此相对位置嵌入的优势在于更好地泛化到长序列和未见过的序列长度。

Transformer中的注意力：

$Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt d_k})V$

式中查询$i$（$Q$ 的第 $i$ 行）和键$j$（$K$ 的第$j$行）之间的交互由点积 $q_i⋅k_j$​ 捕获。绝对位置编码通常在初始嵌入被投影到$Q$ 和$K$ 之前添加。相对位置编码旨在根据相对位置$i-j$ 来修改这种交互。这种相对信息通常可以通过两种主要方式来纳入：

1. 修改注意力得分：可以计算基于相对位置$i−j$的信息，并将其作为偏置项直接添加到$q_i⋅k_j$​的点积中，在 softmax 操作之前。

2. 修改查询/键向量： 查询向量 $q_i$​ 或键向量 $k_j$​（或两者）可以以位置相关的方式进行修改，使得它们的点积隐式地包含相对位置信息。

RoPE

RoPE提供了一种独特方式，将位置信息融入到 Transformer 架构中。不同于通过添加位置向量的绝对位置编码，或通常直接修改注意力分数计算的相对位置编码，RoPE 在注意力分数计算之前，对查询 (q) 和键 (k) 向量应用依赖于位置的旋转。这种方式通过旋转变换巧妙地表示了相对位置信息。

其核心思想源于一个发现：两个分别旋转了 α 和 β 角度的向量之间的点积，取决于它们的原始点积以及角度差 (α−β)。RoPE 运用此特性，设计出依赖于绝对位置的旋转矩阵。

二维向量$q = (x_1,y_1)$和$k=(x_2,y_2)$的内积将其转为复数$(x+y.i)$，再由复数乘法表示：

$q.k=x_1.x_2+y_1.y_2$

复数的乘法计算过程如下：

$q=x_1+y_1i\\ k=x_2+y_2i\\ ⟨q,k⟩=(x_1+y_1i).(x_2+y_2i)\\ =(x_1.x_2-y_1.y_2)+(x_1.y_2+y_1.x_2)i$

可以看到向量内积和复数乘法的实数部分仅相差一个符号，所以我们在复数乘法中，通过共轭复数$k^*=x_2-y_2i$替代$k$，再取乘法实数部分，获得向量内积的结果。

如此一来，二维向量$q_m,k_n$的内积结果可表示如下：

$Re[⟨q_m,k_n^*⟩]=q_m.k_n$

其中$m和n$表示序列中token的绝对位置，$Re[]$表示取结果的实部。二维平面向量$(x_1,x_2)$可由复数表示，对复数乘以$e^{i\theta}$，相当于把该向量逆时针旋转角度$\theta$。只改变了向量的方向，但不改变向量的模长，如下图上部分所示：

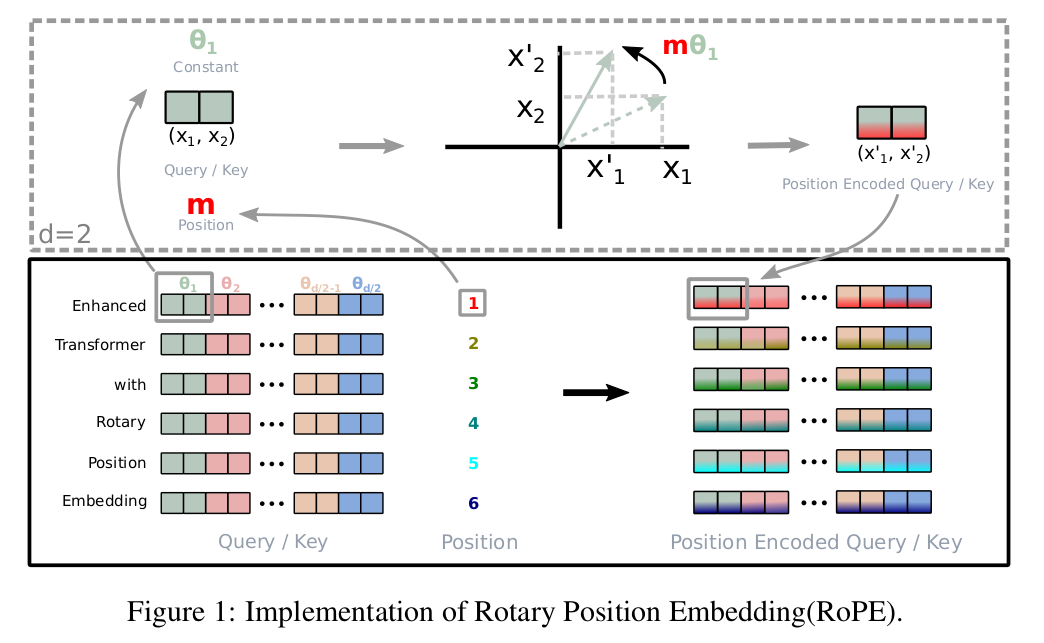
这样做相当于给向量$q_m,k_n$配上了绝对位置编码，然后进行内积，可得：

$q_me^{i\theta}.k_ne^{i\theta}=Re[⟨q_me^{i\theta},(k_ne^{i\theta})^*] ⟩ =Re[q_mk_n^*e^{i\theta} ]$

RoPE在$θ$的选择上，RoPE同样沿用了Transformer位置编码的方案，即$θ=\frac{m-n}{10000^{2i/d}}$，因为它可以带来一定的远程衰减性。

注意$\theta$中的$i$表示向量中的第$i$维，不是虚部

这样一来，就得到了一种融合绝对位置和相对位置于一体的位置编码方案。RoPE同时也巧妙的在Attention计算的QK中将绝对位置和相对位置融合到了一起。使用变换后的Q,K序列做Attention。

$q_m=RoPE(W^Qe_m)\\ k_n=RoPE(W^Ke_n)$

位置信息通过旋转矩阵注入$R_t$，满足结合律：

$q_m^Tk_n =(R_mW^Qe_m)^T(R_nW^Ke_n) =e_m^T(W^Q)^TR^T_mR_nW^Ke_n$

其中$R^T_mR_n$包含了距离是$m-n$的位置信息。QK计算的同时融入了RoPE旋转位置编码

注：标准的注意力机制是$q_mk_n^T$,为什么这里是$q_m^Tk_n$呢？这是因为本文假设的$q,k$是列向量，所以$q_m^Tk_n$才是他的内积，如果假设是行向量，那么就是标准的Attention形式。

$q_me^{i\theta}.k_ne^{i\theta}=Re[⟨q_me^{i\theta},(k_ne^{i\theta})^*] ⟩ =Re[q_mk_n^*e^{i\theta} ]$

对于二维实数向量$q(x,y)$,在实际的计算中把$e^{i\theta}$幂函数进行恒等转换，由欧拉公式：

$e^{i\theta}=cos\theta+sin\theta.i$

其中e是自然对数的底，i是虚数单位。它将三角函数与复指数函数关联起来，因此：

$qe^{i\theta}=(x+yi)e^{i\theta} \\=(x+yi)(cos\theta+sin\theta.i)\\ =(xcos\theta-ysin\theta)+(xsin\theta+ycos\theta)i\\$

这样就将幂函数的计算转化为了三角函数的计算。到这里，就完成了二维向量的RoPE的位置编码。

接下来针对二维实向量

$q = \begin{Bmatrix} q^{(1)} \\ q^{(2)} \end{Bmatrix}, k = \begin{Bmatrix} k^{(1)} \\ k^{(2)} \end{Bmatrix}$

其复数形式为$q_m=q^{(1)}+iq^{(2)}，k_n=k^{(1)}+ik^{(2)}$，$θ=\frac{m-n}{10000^{2i/d}}$，由欧拉公式展开后仅保留实部转化后的复数域内积为：

$Re[q_mk_n^*e^{i\theta} ]=(q^{(1)} \ q^{(2)}) \begin{pmatrix} cos\theta & -sin\theta \\sin\theta & cos\theta \end{pmatrix} \begin{pmatrix} k^{(1)}\\ k^{(2)} \end{pmatrix}$

$q_m,k_m$分别用欧拉公式转化后的旋转矩阵

$R_m =\begin{pmatrix} cos \frac{m}{10000^{2i/d}} & -sin\frac{m}{10000^{2i/d}} \\ sin\frac{m}{10000^{2i/d}}& cos\frac{m}{10000^{2i/d}} \end{pmatrix}$

$R_n =\begin{pmatrix} cos \frac{n}{10000^{2i/d}} & -sin\frac{n}{10000^{2i/d}} \\ sin\frac{n}{10000^{2i/d}} & cos\frac{n}{10000^{2i/d}} \end{pmatrix}$

且：

$R^T_mR_n=\begin{pmatrix} cos \frac{m-n}{10000^{2i/d}} & -sin\frac{m-n}{10000^{2i/d} }\\sin\frac{m-n}{10000^{2i/d}} & cos\frac{m-n}{10000^{2i/d}} \end{pmatrix}$

所以二维向量对应的RoPE计算公式为：

$Re[q_mk_n^*e^{i\theta} ] = q^TR^T_mR_nk\\ =(q^{(1)} \ q^{(2)}) \begin{pmatrix} cos \frac{m-n}{10000^{2i/d}} & -sin\frac{m-n}{10000^{2i/d}} \\sin\frac{m-n}{10000^{2i/d}} & cos\frac{m-n}{10000^{2i/d}} \end{pmatrix} \begin{pmatrix} k^{(1)}\\ k^{(2)} \end{pmatrix}\\ = (q^{(1)} \ q^{(2)}) \begin{pmatrix} cos \theta & -sin\theta \\sin\theta & cos\theta \end{pmatrix} \begin{pmatrix} k^{(1)}\\ k^{(2)} \end{pmatrix}\\$

与复数域内积计算完全一致。

代码实现时，常用实数矩阵旋转（直接用三角函数算）

理论推导时，常用复数旋转

两种实现，最终都是让注意力分数里隐含位置差，让模型记住语序信息

但是这种变换仅适用于二维向量，而真实场景中都是高维向量，所以直观的想法就是将高维向量拆分成多个二维向量的拼接每两个二维向量之间做内积。设$q$（Attention中的$q$）的位置向量长度为$d$，每两个元素为一组二维向量，一共有$d/2$个组合，可以直接拼接作为$d$维度的旋转位置编码。(k同理)

$\begin{pmatrix} cos \theta_0 & -sin\theta_0 & 0 & 0&... &0&0\\ sin\theta_0 & cos\theta_0 & 0 & 0&... &0&0 \\ 0 & 0&cos \theta_1 & -sin\theta_1 & ... &0&0 \\ 0 & 0& sin\theta_1 & cos\theta_1 & ... &0&0 \\ ...&...&...&...&...&...&...& \\ 0&0&0&0&...& cos \theta_{d/2-1} & -sin\theta_{d/2-1}\\ 0&0&0&0&...&sin\theta_{d/2-1}&cos \theta_{d/2-1} \end{pmatrix} \begin{pmatrix} q_0\\q_1\\q_2\\q_3\\...\\...\\q_{d-1}\\ \end{pmatrix}$

其中$\theta_n=\frac{n}{10000^{2n/d}},n\in {0,1,2,...,d-1 }$

既然向量拆分了，那就可以采用分块矩阵来进行变换，每个块只关注两个分量的信息，且每个块的幅角也可以不同。因为采用矩阵相乘的方式来实现RoPE会浪费很多显存，所以在实际计算中采用逐位相乘的方式来实现 RoPE：

$\begin{pmatrix} q_0\\q_1\\q_2\\q_3\\...\\...\\q_{d-1}\\ \end{pmatrix} \otimes \begin{pmatrix} cos \theta_0\\cos \theta_0\\cos \theta_1\\cos \theta_1\\...\\cos \theta_{d/2-1}\\cos \theta_{d/2-1} \end{pmatrix} + \begin{pmatrix} -q_1\\q_0\\-q_3\\q_4\\...\\-q_{d-1}\\q_{d-2}\\ \end{pmatrix} \otimes \begin{pmatrix} sin\theta_0\\sin\theta_0\\sin\theta_1\\sin\theta_1\\...\\sin\theta_{d/2-1}\\sin\theta_{d/2-1}\\ \end{pmatrix}$

同时RoPE是目前唯一一种可以用于线性Attention的相对位置编码。这是因为其他的相对位置编码，都是直接基于Attention矩阵进行操作的，但是线性Attention并没有事先算出Attention矩阵，因此也就不存在操作Attention矩阵的做法，所以其他的方案无法应用到线性Attention中。而对于RoPE来说，它是用绝对位置编码的方式来实现相对位置编码，不需要操作Attention矩阵，因此有了应用到线性Attention的可能性。

线性Attention的常见形式：

$Attention(Q,K,V)_i =\frac{\sum^n_{j=1}sim(q_i,k_j)v_j}{\sum^n_{j=1}sim(q_i,k_j)} =\frac{\sum^n_{j=1}ϕ(q_i)^⊤φ(k_j)v_j}{\sum^n_{j=1}ϕ(q_i)^⊤φ(k_j)}$

其中$ϕ,φ$是值域非负的激活函数

RoPE实现代码

Roformer的实现，完整的代码在这里，其中RoPE计算的核心功能如下，使用了逐位相乘的形式：

def apply_rotary_position_embeddings(sinusoidal_pos, query_layer, key_layer, value_layer=None):
    # https://kexue.fm/archives/8265
    # sin [batch_size, num_heads, sequence_length, embed_size_per_head//2]
    # cos [batch_size, num_heads, sequence_length, embed_size_per_head//2]
    sin, cos = sinusoidal_pos.chunk(2, dim=-1)
    # sin [θ0,θ1,θ2......θd/2-1] -> sin_pos [θ0,θ0,θ1,θ1,θ2,θ2......θd/2-1,θd/2-1]
    sin_pos = torch.stack([sin, sin], dim=-1).reshape_as(sinusoidal_pos)
    # cos [θ0,θ1,θ2......θd/2-1] -> cos_pos [θ0,θ0,θ1,θ1,θ2,θ2......θd/2-1,θd/2-1]
    cos_pos = torch.stack([cos, cos], dim=-1).reshape_as(sinusoidal_pos)
    # rotate_half_query_layer [-q1,q0,-q3,q2......,-qd-1,qd-2]
    rotate_half_query_layer = torch.stack([-query_layer[..., 1::2], query_layer[..., ::2]], dim=-1).reshape_as(
        query_layer
    )
    query_layer = query_layer * cos_pos + rotate_half_query_layer * sin_pos
    # rotate_half_key_layer [-k1,k0,-k3,k2......,-kd-1,kd-2]
    rotate_half_key_layer = torch.stack([-key_layer[..., 1::2], key_layer[..., ::2]], dim=-1).reshape_as(key_layer)
    key_layer = key_layer * cos_pos + rotate_half_key_layer * sin_pos
    if value_layer is not None:
        # rotate_half_value_layer [-v1,v0,-v3,v2......,-vd-1,vd-2]
        rotate_half_value_layer = torch.stack([-value_layer[..., 1::2], value_layer[..., ::2]], dim=-1).reshape_as(
            value_layer
        )
        value_layer = value_layer * cos_pos + rotate_half_value_layer * sin_pos
        return query_layer, key_layer, value_layer
    return query_layer, key_layerch_size, seq_len, d_model)
        return output

参考文献

[1] Transformer升级之路：1、Sinusoidal位置编码追根溯源 - 科学空间|Scientific Spaces

[2] Transformer升级之路：2、博采众长的旋转式位置编码 - 科学空间|Scientific Spaces

[3] Understanding Positional Embeddings in Transformers: From Absolute to Rotary | Towards Data Science

[4] 介绍 RoPE 旋转位置编码