威伦特

递归神经网络（Recurrent Neural Network, RNN）是一种专门处理序列的神经网络。它们通常用于自然语言处理(NLP） 任务，因为RNN在处理文本方面非常有效。

第一句话：我喜欢吃苹果！

第二句话：苹果真是一家很棒的公司！

如果任务是要给苹果打标签，RNN就结合上下文去训练模型，能够准确识别出第一个苹果是一种水果，第二个是苹果公司，

RNN能够将可变长度序列作为输入和输出

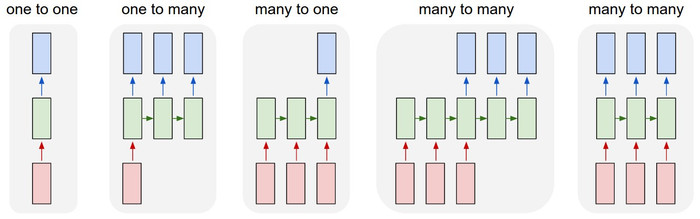
• 固定大小的输入到固定大小的输出（例如图像分类）。
• 序列输出（例如，从图像字幕生成）。
• 序列输入（例如，句子情感分析）。
• 序列输入和序列输出（例如机器翻译）。
• 同步序列输入和输出（例如，视频分类）

实现过程

正向传播：

如果使用一个“多对一”的RNN，来进行情感分析，即输入词向量$\ x_0,x_1,...,x_n，获得y$属于正向\负向情感的概率

如下图：

RNN的计算遵循如下规则：

• 下一个隐藏状态是使用上一个隐藏状态和下一个输入决定的

  $\ h_t=tanh(W_{xh}x_t+W_{hh}h_{t-1}+b_h)$，式子中使用了tanh作为激活函数

• 输出向量y由h所决定

  $\ y_t=W_{ht}h_t+b_y$

其中，$\ W_{xh}$为用来链接**$\ x→h$的权重，$\ W_{hh}$用来链接$\ h_n→h_{n+1}$的权重，$\ W_{hy}$用来链接$\ h_t→y_t$** 的权重，

$\ b_{h}用来链接$$\ x→h$的偏差,$\ b_{y}$用来链接 $\ h→y$ 的偏差

反向传播

训练RNN权重参数，首先需要一个损失函数。通常使用Softmax与交叉熵损失函数，作为损失函数。

$L=-ln(softmax(y_c))=-ln\frac{e^{y_c}}{\sum_je^{y_j}}$

将L对y进行求导：

$\frac{∂L}{∂y_i}=\begin{cases} softmax(y_i),\quad i\neq c\\ softmax(y_i)-1, \quad i=c \end{cases} \tag{1}$

例如，如 softmax(y) = [0.2,0.2,0.6],正确的类别为 0 ,那么对L求导得到：[-0.8， 0.2， 0.6]

再将L分别对RNN中所有参数进行求导：

$由于：y_t=W_{ht}h_t+b_y,\\h_t=tanh(W_{xh}x_t+W_{hh}h_{t-1}+b_h)\\$

$\frac{∂L}{∂W_{hy}}=\frac{∂L}{∂y}*\frac{∂y}{∂W_{hy}}=\frac{∂L}{∂y}*h_n \tag {2}$

$\frac{∂L}{∂b_{hy}}=\frac{∂L}{∂y}*\frac{∂y}{∂b_{y}}=\frac{∂L}{∂y}\tag {3}$

因为变化$\ W_{xh}$会影响每一个$\ h_n$，这都会影响最终的损失函数，因此我们需要将每个时间的梯度都计算出来然后加起来，作为每次$\ W_{xh}$更新的梯度值，这称为时序反向传播算法（BPTT）

$\frac{∂L}{∂W_{xh}}=\frac{∂L}{∂y}\sum_t\frac{∂y}{∂h_t}*\frac{∂h_t}{∂W_{xh}} \tag 4$

$\frac{∂h_t}{∂W_{xh}} =\frac{∂\ h_t}{∂(W_{xh}x_t+W_{hh}h_{t-1}+b_h)}*\frac{∂(W_{xh}x_t+W_{hh}h_{t-1}+b_h)}{∂W_{xh}}\\ =(1-tanh^2(W_{xh}x_t+W_{hh}h_{t-1}+b_h))*x_t\\ =(1-h_t^2)x_t \tag {5}$

同样得到：

$\frac{∂h_t}{∂W_{hh}}=(1-h_t^2)h_{t-1} \tag 6$

$\frac{∂h_t}{∂b_{h}}=(1-h_t^2) \tag7$

$\frac{∂y}{∂h_{t}}=\begin{cases} \frac{∂y}{∂h_{t+1}}*(1-h_t^2)W_{hh} \quad t\neq n\\ W_{hy}\quad t=n \end{cases} \tag 8$

联合①⑤⑧得到$\ {∂L}/{∂W_{xh}}$

联合①⑥⑧得到$\ {∂L}/{∂W_{hh}}$

联合①⑦⑧得到$\ {∂L}/{∂b_{h}}$

梯度下降

计算完所有梯度后，使用梯度下降来更新权重和偏差。

$W_{hh}= W_{hh}-\mu\frac{∂L}{∂W_{hh}}\\ W_{xh}= W_{xh}-\mu\frac{∂L}{∂W_{xh}}\\ W_{hy}= W_{hy}-\mu\frac{∂L}{∂W_{hy}}\\ b_{h}= b_{h}-\mu\frac{∂L}{∂b_{h}}\\ b_{y}= b_{y}-\mu\frac{∂L}{∂b_{y}}\\$

代码

# This is a simple demo for using RNN to predict the phrases sentiment in the dataset.
import numpy as np
from database import test_data, train_data
from numpy import random

'''
Dimension of vector:
h=[64,1]
why[2,64]
whh[64,64]
wxh[2,64]
bh[64,1]
by[2,1]
y=[2,1]
'''


class RNN:
    def __init__(self, input_size, output_size, hidden_size=64):
        # Define hidden layer has 64 neurons
        self.Whh = random.randn(hidden_size, hidden_size) / 1000
        self.Wxh = random.randn(hidden_size, input_size) / 1000
        self.Why = random.randn(output_size, hidden_size) / 1000
        self.bh = np.zeros((hidden_size, 1))
        self.by = np.zeros((output_size, 1))
        self.last_hs = {}
        self.last_inputs = []

    def forward(self, inputs):
        h = np.zeros((self.Whh.shape[0], 1))
        self.last_inputs = inputs
        self.last_hs = {0: h}
        for i, x in enumerate(inputs):
            h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)
            self.last_hs[i + 1] = h
        # enumerate:枚举  @:矩阵的乘法
        y = self.Why @ h + self.by
        return y

    def backprop(self, d_y, learn_rate=2e-2):
        n = len(self.last_inputs)
        d_Why = d_y @ self.last_hs[n].T
        d_Whh = np.zeros(self.Whh.shape)
        d_Wxh = np.zeros(self.Wxh.shape)
        d_bh = np.zeros(self.bh.shape)
        d_by = d_y
        # Calculate dL/dh for the last h.
        d_h = self.Why.T @ d_y
        for t in reversed(range(n)):
            temp = ((1 - self.last_hs[t + 1] ** 2) * d_h)
            d_bh += temp
            d_Whh += temp @ self.last_hs[t].T
            d_Wxh += temp @ self.last_inputs[t].T
            d_h = self.Whh @ temp
        # Make the values between -1 and 1
        for d in [d_Wxh, d_Whh, d_Why, d_bh, d_by]:
            np.clip(d, -1, 1, out=d)
        # Using gradient descent to update the weights and biases
        self.Whh -= learn_rate * d_Whh
        self.Wxh -= learn_rate * d_Wxh
        self.Why -= learn_rate * d_Why
        self.bh -= learn_rate * d_bh
        self.by -= learn_rate * d_by


def softMax(x):
    return np.exp(x) / sum(np.exp(x))


def createInputs(text):
    # Returns one-hot vectors representing the words in the input text

    inputs = []
    for w in text.split(' '):
        v = np.zeros((vocab_size, 1))
        v[word_to_idx[w]] = 1
        inputs.append(v)
    return inputs


def processData(data, backprop=True):
    items = list(data.items())
    random.shuffle(items)  # shuffle:random arrangement the order of the list
    loss = 0
    num_correct = 0
    for x, y in items:
        inputs = createInputs(x)
        target = int(y)
        out = rnn.forward(inputs)
        prob = softMax(out)
        loss += (-np.log(prob[target]))
        num_correct += int(np.argmax(prob) == target)  # argmax :index of the max value
        if backprop:
            # get DL\Dy
            d_y = prob
            d_y[target] -= 1

            rnn.backprop(d_y)
    return loss / len(data), num_correct / len(data)


if __name__ == '__main__':
    # Generate "one-hot" word vector
    vocab = list(set([w for text in train_data.keys() for w in text.split(' ')]))
    vocab_size = len(vocab)
    word_to_idx = {w: i for i, w in enumerate(vocab)}
    idx_to_word = {i: w for i, w in enumerate(vocab)}
    # Generate rnn
    rnn = RNN(input_size=len(vocab), output_size=2)
    print("负情感" if np.argmax(softMax(rnn.forward(createInputs("i am not earlier")))) == 0 else "正情感")
    for epoch in range(1000):
        train_loss, train_acc = processData(train_data)
        if epoch % 100 == 99:
            print(f'--- Epoch {epoch + 1}')
            print(f'Train Loss: {np.round(train_loss, 3)} | Accuracy: {np.round(train_acc, 3)}')
            test_loss, test_acc = processData(test_data, backprop=False)
            print(f'Test Loss: {np.round(test_loss, 3)} | Accuracy: {np.round(test_acc, 3)}')
    print("负情感"if np.argmax(softMax(rnn.forward(createInputs("i am not earlier"))))==0 else "正情感")

简单的数据集：

train_data = {
  'good': True,
  'bad': False,
  'happy': True,
  'sad': False,
  'not good': False,
  'not bad': True,
  'not happy': False,
  'not sad': True,
  'very good': True,
  'very bad': False,
  'very happy': True,
  'very sad': False,
  'i am happy': True,
  'this is good': True,
  'i am bad': False,
  'this is bad': False,
  'i am sad': False,
  'this is sad': False,
  'i am not happy': False,
  'this is not good': False,
  'i am not bad': True,
  'this is not sad': True,
  'i am very happy': True,
  'this is very good': True,
  'i am very bad': False,
  'this is very sad': False,
  'this is very happy': True,
  'i am good not bad': True,
  'this is good not bad': True,
  'i am bad not good': False,
  'i am good and happy': True,
  'this is not good and not happy': False,
  'i am not at all good': False,
  'i am not at all bad': True,
  'i am not at all happy': False,
  'this is not at all sad': True,
  'this is not at all happy': False,
  'i am good right now': True,
  'i am bad right now': False,
  'this is bad right now': False,
  'i am sad right now': False,
  'i was good earlier': True,
  'i was happy earlier': True,
  'i was bad earlier': False,
  'i was sad earlier': False,
  'i am very bad right now': False,
  'this is very good right now': True,
  'this is very sad right now': False,
  'this was bad earlier': False,
  'this was very good earlier': True,
  'this was very bad earlier': False,
  'this was very happy earlier': True,
  'this was very sad earlier': False,
  'i was good and not bad earlier': True,
  'i was not good and not happy earlier': False,
  'i am not at all bad or sad right now': True,
  'i am not at all good or happy right now': False,
  'this was not happy and not good earlier': False,
}

test_data = {
  'this is happy': True,
  'i am good': True,
  'this is not happy': False,
  'i am not good': False,
  'this is not bad': True,
  'i am not sad': True,
  'i am very good': True,
  'this is very bad': False,
  'i am very sad': False,
  'this is bad not good': False,
  'this is good and happy': True,
  'i am not good and not happy': False,
  'i am not at all sad': True,
  'this is not at all good': False,
  'this is not at all bad': True,
  'this is good right now': True,
  'this is sad right now': False,
  'this is very bad right now': False,
  'this was good earlier': True,
  'i was not happy and not good earlier': False,
}

运行结果

正情感
--- Epoch 100
Train Loss: [0.688] | Accuracy: 0.552
Test Loss: [0.699] | Accuracy: 0.5
...
--- Epoch 1000
Train Loss: [0.002] | Accuracy: 1.0
Test Loss: [0.004] | Accuracy: 1.0
负情感

在训练了1000代后，能够正确的预测结果了