朴素贝叶斯在sklearn中的实现
朴素贝叶斯方法是基于贝叶斯定理的一组有监督学习算法，给定一个类别y和一个从x_1到x_n的相关的特征向量， 贝叶斯定理公式表示如下:
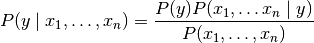
假设每个特征之间都相互独立：
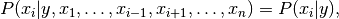
于是公式可以简化为
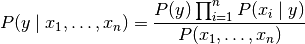
由于在给定的输入中 
是一个常量，我们使用下面的分类规则:
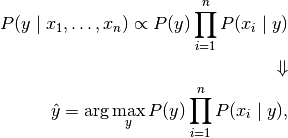
可以使用最大后验概率来估计 P(y)和 P(x_i \y) ; 前者是训练集中类别 y的相对频率。
虽然朴素贝叶斯分类的效果很好，但却不是好的估计器，所以不能太过于重视从 predict_proba 输出的概率。
朴素贝叶斯的分类
在sklearn中，一共有3个朴素贝叶斯的分类算法，分别是GaussianNB,MultinomialNB和BernoulliNB
GAUSSIANNB（高斯贝叶斯）
GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)服从正态分布:
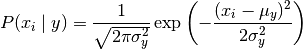
其中，σ_y参数和μ_y 使用最大似然法估计。
通过鸢尾花数据集作为例子，使用sklearn实现GAUSSIANNB
鸢尾花数据集
提取码：1234
首先对数据集进行提取，输出前几行进行查看：
column_names=['SepalLength','SepalWidth','PetalLength','PetalWidth','Species']
data=pandas.read_csv('./iris_training.csv',header=0,names=column_names)
print(data.head(3))
| SepalLength | SepalWidth | PetalLength | PetalWidth | Species |
|---|---|---|---|---|
| 6.4 | 2.8 | 5.6 | 2.2 | 2 |
| 5.0 | 2.3 | 3.3 | 1.0 | 1 |
| 4.9 | 2.5 | 4.5 | 1.7 | 2 |
鸢尾花数据集的标签一共是3种，代表三种鸢尾花
测试集给出一朵花的4个特征，判断是属于哪类鸢尾花
接下来切分数据集，前25行为训练数据，其余为测试数据
npData=np.array(data)
train_data=npData[:25,0:4]
train_label=npData[:25,4]
predict_data=npData[25:,0:4]
predict_label=npData[25:,4]
Xtrain=train_data
Ytrain=train_label
Xtest=predict_data
Ytest=predict_label
接下来调用相关函数进行计算
clf=GaussianNB()
clf.fit(Xtrain,Ytrain)
predict = clf.predict(Xtest)
print(predict)
prob = clf.predict_proba(Xtest)
print(prob)
print(clf.score(Xtest,Ytest))
其中：
clf.predict() 输出为每一组数据进行分类的类别
[0. 1. 2. 1. 2. 1. 1. 1. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 0. 1. 0. 2. 0.
1. 0. 1. 1. 0. 1. 2. 2. 2. 2. 1. 1. 2. 2. 2. 1. 2. 0. 2. 2. 0. 0. 1. 0.
2. 2. 0. 1. 1. 1. 2. 0. 1. 1. 1. 2. 0. 1. 1. 1. 0. 2. 1. 0. 0. 2. 0. 0.
3. 2. 0. 0. 1. 0. 1. 0. 0. 0. 0. 1. 0. 2. 1. 0. 2. 0. 1. 1. 0. 0. 1.]
clf.predict_proba() 输出为预测的准确率
0.968421052631579
clf.score(Xtest,Ytest)输出为每组数据在各类别的概率
[[1.00000000e+000 1.03276921e-014 1.04755718e-021]
[1.52220777e-067 9.99638109e-001 3.61891415e-004]
[1.52662245e-147 7.71337608e-002 9.22866239e-001]
[3.46657230e-100 9.79212770e-001 2.07872298e-002]
[1.65108983e-138 1.49010121e-001 8.50989879e-001]
[2.18363297e-090 9.96165314e-001 3.83468595e-003]
[6.60011077e-030 9.99998455e-001 1.54475084e-006]
[3.03504780e-101 9.22883269e-001 7.71167310e-002]
[6.52533913e-193 7.26844383e-005 9.99927316e-001]
[2.26774333e-131 2.05158029e-001 7.94841971e-001]
[9.67885119e-220 6.61707470e-007 9.99999338e-001]
[3.79233963e-160 2.17314809e-003 9.97826852e-001]
...]
MULTINOMIALNB(多项分布朴素贝叶斯)
它的假设特征是由一个简单多项式分布生成。多项分布可以描述各种类型样本出行次数的频率，因此多项式朴素贝叶斯非常适合用于描述出现次数或者出现次数比例的特征。
该模型常用于文本分类，特征表示的是次数，例如某个词语的出现次数
分布参数由每类 y的 θ_y=(θ_y_1,...,θ_yn ) 向量决定 ,式中 n是特征的数量(对于文本分类，是词汇量的大小) θ_yi是样本中属于类 y 中特征 i 概率 P(x_i|y) 。
参数θ_y 使用平滑过的最大似然估计法来估计，即相对频率计数:
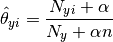
式中N_yi是 训练集 T 中特征 i 在类 y 中出现的次数，N_y 是类 y 中出现所有特征的计数总和。
先验平滑因子α≥0 为在学习样本中没有出现的特征而设计，以防在将来的计算中出现0概率输出。 把 α=1被称为拉普拉斯平滑，而 α< 1 被称为Lidstone平滑。
通过新闻分类数据集作为例子，使用sklearn实现MULTINOMIALNB
新闻分类数据集
提取码：sky5
所用新闻数据集包含 train 训练集, test 测试集 数据两个文件夹，两个文件夹下各包含 四个子文件夹，代表1，2，3，4 四类新闻的文件，每条新闻的txt 文件存放在此四类文件夹中。
首先对数据集进行提取
trainData1="./text/train/1"
trainData2="./text/train/2"
trainData3="./text/train/3"
trainData4="./text/train/4"
newsData1='./text/test/1'
newsData2='./text/test/2'
newsData3='./text/test/3'
newsData4='./text/test/4'
def preData(trainData,type):
files=os.listdir(trainData)
file_news=[]
for file in files:
path=trainData+'/'+file
with open(path,'r') as f:
news=f.readlines()
file_news.append(news[0].strip())
df=pandas.DataFrame({'news':file_news,'Newstype':[type for i in range(len(file_news))]})
return df
trainType1=preData(trainData1,1)
trainType2=preData(trainData2,2)
trainType3=preData(trainData3,3)
trainType4=preData(trainData4,4)
trainData=pandas.concat([trainType1,trainType2,trainType3,trainType4])
train_size=len(trainData)
test_data=pandas.concat([preData(newsData1,1),preData(newsData2,2),preData(newsData3,3),preData(newsData4,4)])
接下来对训练数据和测试数据进行去重，重置索引
test_data=test_data.drop_duplicates()
testData=test_data.reset_index(drop=True)
train_data=train_data.drop_duplicates()
trainData=train_data.reset_index(drop=True)
查看数据
接下来对数据进行jieba分词，提取tf-idf值，并转为向量
with open('./stopword.txt','r') as stop:
stopwords=stop.readlines()
stopwords=[i.strip() for i in stopwords]
def cutword(word):
res=[]
jie=jieba.lcut(word)
for i in jie:
if(i not in stopwords) and (i!=''):
res.append(i.strip())
return res
testData.news=testData.news.apply(cutword)
testData.news=testData.news.apply(lambda x: ' '.join([i for i in x if i !='']))
trainData.news=trainData.news.apply(cutword)
trainData.news=trainData.news.apply(lambda x: ' '.join([i for i in x if i !='']))
#apply() 函数可以作用于整个 DataFrame，功能也是自动遍历整个DataFrame,
# 对每一个元素运行指定的函数。
tf_idf=TfidfVectorizer()
train_tf_idfMaritx=tf_idf.fit_transform(trainData.news)
test_tf_idfMaritx=tf_idf.transform(testData.news)
train_tf_idfarray=train_tf_idfMaritx.toarray()
test_tf_idfarray=test_tf_idfMaritx.toarray()
trainData=np.array(trainData)
testData=np.array(testData)
分词及TF-IDF如下
切分数据，进行MULTINOMIALNB
x_train=train_tf_idfarray
y_train=trainData[:,1]
x_test=test_tf_idfarray
y_test=testData[:,1]
MNB=MultinomialNB(alpha=0.1)
MNB.fit(x_train,y_train.astype('int'))
MNB.predict(x_test)
prob = MNB.predict_proba(x_test)
print(prob)
predict = MNB.predict(x_test)
模型预测正确率为：0.898989898989899
评估预测效果
mat = confusion_matrix(y_test.astype('int'),predict) #混淆矩阵
df = pd.DataFrame(mat,columns=[1,2,3,4],index=[1,2,3,4])
report_MNB = classification_report(y_test.astype('int'),predict)
print(report_MNB)
混淆矩阵：
[[ 35 1 2 0]
[ 4 105 3 1]
[ 0 2 29 0]
[ 0 4 3 9]]
precision recall f1-score support
1 0.90 0.92 0.91 38
2 0.94 0.93 0.93 113
3 0.78 0.94 0.85 31
4 0.90 0.56 0.69 16
accuracy 0.90 198
macro avg 0.88 0.84 0.85 198
weighted avg 0.90 0.90 0.90 198
模型对 1、2、3 类的 预测效果较好而对第四类预测效果不佳，是因为训练数据集中第四类数据太少。
因此，在使用MULTINOMIALNB时候要注意让各类别文本数量接近
BERNOULLINB（伯努利贝叶斯）
BernoulliNB 实现了用于多重伯努利分布数据的朴素贝叶斯训练和分类算法，即有多个特征，但每个特征 都假设是一个二元 (Bernoulli, boolean) 变量。 因此，这类算法要求样本以二元值特征向量表示；如果样本含有其他类型的数据， 一个 BernoulliNB 实例会将其二值化(取决于 binarize 参数)。
伯努利朴素贝叶斯的决策规则基于:
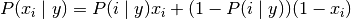
与多项分布朴素贝叶斯的规则不同 伯努利朴素贝叶斯明确地惩罚类 y 中没有出现作为预测因子的特征 i ，而多项分布分布朴素贝叶斯只是简单地忽略没出现的特征。
通过识别手写数字数据集作为例子，使用sklearn实现BERNOULLINB
它包含了四个部分:
- Training set images: train-images-idx3-ubyte.gz (9.9 MB, 解压后 47 MB, 包含 60,000 个样本)
- Training set labels: train-labels-idx1-ubyte.gz (29 KB, 解压后 60 KB, 包含 60,000 个标签)
- Test set images: t10k-images-idx3-ubyte.gz (1.6 MB, 解压后 7.8 MB, 包含 10,000 个样本)
- Test set labels: t10k-labels-idx1-ubyte.gz (5KB, 解压后 10 KB, 包含 10,000 个标签)
数据的读取与存储
将下载好的数据解压带代码目录下即可。
数据文件时二进制格式的，所以要按字节读取。
import struct
from PIL import Image
from array import array as pyarray
from numpy import array, int8, uint8, zeros
trainImagePath='./手写数字数据集/train-images.idx3-ubyte'
testImagePath='./手写数字数据集/t10k-images.idx3-ubyte'
trainLabelPath='./手写数字数据集/train-labels.idx1-ubyte'
testLabelPath='./手写数字数据集/t10k-labels.idx1-ubyte'
def readData(imagePath,labelPath):
digits = np.arange(10)
data = open(labelPath, 'rb')
magic_nr, size = struct.unpack(">II", data.read(8))
label=pyarray('b',data.read())
data.close()
data2 = open(imagePath, 'rb')
magic_nr, size, rows, cols = struct.unpack(">IIII", data2.read(16))
img = pyarray("B", data2.read())
data2.close()
ind = [k for k in range(size) if label[k] in digits]
N = len(ind)
images = zeros((N, rows * cols), dtype=uint8)
labels = zeros((N, 1), dtype=int8)
for i in range(len(ind)):
images[i] = array(img[ind[i] * rows * cols: (ind[i] + 1) * rows * cols]).reshape((1, rows * cols))
labels[i] = label[ind[i]]
return images,labels
读取后的image和label数据都为二维数组，image里每个元素为784维的向量，对应为28*28的图形
将数据通过图片表示
接下来将784维的向量转化为28*28的二维数组，再将二维数组通过灰度图表示出来
下面将前五个元素进行灰度图的转化
def showImage(image,label):
for i in range(5):
a = np.array(image[i])
a=a.reshape((28,28))
im = Image.fromarray(a)
im = im.convert('L') # 这样才能转为灰度图，如果是彩色图则改L为‘RGB’
im.save('finger{}.png'.format(label[i]))
结果如下：
接下来调用BernoulliNB进行预测
trainImage,trainLabel=readData(trainImagePath,trainLabelPath)
trainLabel=np.array(trainLabel).reshape(-1)#将二维数组转为一维
testImage,testLabel=readData(testImagePath,testLabelPath)
# showImage(trainImage,trainLabel)
bnb=BernoulliNB()
bnb.fit(trainImage,trainLabel)
predict=bnb.predict(testImage)
print("accuracy_score: %.4lf" % accuracy_score(predict,testLabel))
print("Classification report for classifier %s:\n%s\n" % (bnb, classification_report(testLabel, predict)))
Classification report for classifier BernoulliNB():
precision recall f1-score support
0 0.91 0.91 0.91 980
1 0.90 0.96 0.93 1135
2 0.89 0.83 0.86 1032
3 0.76 0.84 0.80 1010
4 0.83 0.81 0.82 982
5 0.82 0.70 0.76 892
6 0.89 0.89 0.89 958
7 0.93 0.85 0.89 1028
8 0.75 0.78 0.77 974
9 0.75 0.84 0.79 1009
accuracy 0.84 10000
macro avg 0.84 0.84 0.84 10000
weighted avg 0.84 0.84 0.84 10000
accuracy_score: 0.8413
总结
朴素贝叶斯推断的优点：
- 生成式模型，通过计算概率来进行分类，可以用来处理多分类问题
- 对小规模的数据表现很好，算法简单，适合增量式训练
朴素贝叶斯推断的缺点：
- 对输入数据的表达形式很敏感
- 由于朴素贝叶斯的“朴素”特点，所以会带来精确率上的损失
- 需要计算先验概率，分类决策存在错误率
- 并不是好的估计器
三种朴素贝叶斯的适用场景：
- GAUSSIANNB是一种特殊类型的NB算法,它特别用于当特征具有连续值时，同时假定所有特征符合高斯分布，比如通过升高和体重预测性别中，由于升高和体重特征值都是连续的数值。
- MULTINOMIALNB多用于离散特征分类，例如文本分类单词统计，以出现的次数作为特征值。
- BERNOULLINB与多项式贝叶斯模型一样，伯努利朴素贝叶斯适用于离散特征情况，只是伯努利模型中每个特征的取值必须为0或1。例如在文档中特征是单词是否出现
参考
- https://blog.csdn.net/weixin_44264662/article/details/90700399 《机器学习实战》学习笔记（五） ： sklearn中关于朴素贝叶斯的用法
- https://www.sklearncn.cn/10/ 《朴素贝叶斯》
- https://blog.csdn.net/weixin_47176703/article/details/124304692 python-新闻文本分类详细案例
- https://blog.csdn.net/haohuang_ch/article/details/81297410 sklearn之分类算法与手写数字识别