威伦特

解码生命

首页 文章 标签 关于

MoCa

2023-02-22 7 min read # NLP

BRIO在生成式文本摘要领域SOTA位置还没坐稳几个月，便出现了新的SOTA—MoCa

概述

在上一篇文章中说明了BRIO这个在文本摘要抽取领域的训练新范式，BRIO通过利用对比学习（contrastive learning）来构建一个评估模型，让候选的分布的也成为优化目标的一部分，将预训练模型和评估模型一起训练。从而解决了传统的基于极大似然估计训练而造成 曝光偏差(exposure bias) 的问题，

而MoCa(Momentum Calibration for Text Generation)就是基于BRIO提出的预训练+评估的基础上进一步的优化与改进，并在多个数据集取得了新的SOTA效果

MoCa训练流程

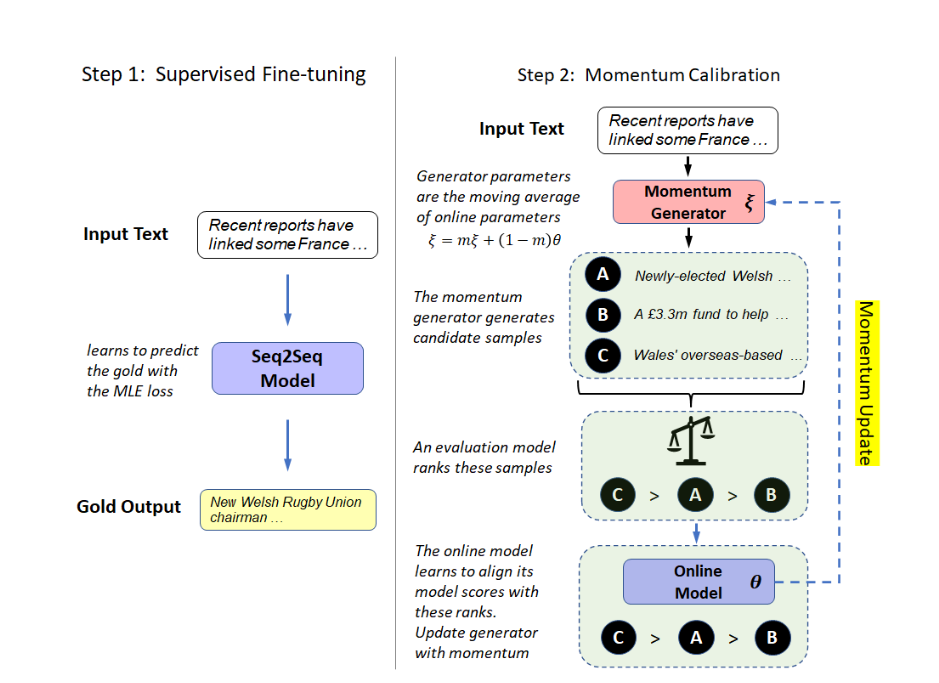
下图左边是传统的训练方式，右边是MoCa的训练方式

MoCa大体的训练流程如下：

  • 首先通过Momentum来初始化生成模型的参数

  • 首先将数据集中的文本输入到生成模型中，将beam Search设置为16，输出16个候选摘要

  • 再将16个候选摘要通过评估模型进行重要性排序（可以是ROUGE、BLUE、BERTScore等评估方式）

  • 在线模型学习将其样本在模型的分数与这些排名对齐。

  • 接下来构建损失函数，联立在线模型和生成模型一起优化

MoCa

MoCa由两个模型构成，一个是生成模型G(ξ)，一个是在线模型M(θ)，它们共享相同的模型体系结构，但有自己的参数。在训练开始时，设置ξ = θ。

样本生成

首先在生成模型G(ξ)中，给定输入序列 X\ X，然后通过beam search或者diverse beam search生成K个样本 Y1，Y2,...,Yk\ Y_1，Y_2,...,Y_k。

作者在论文也说明了为什么使用BS或DBS而不使用sampling或nucleus sampling来生成候选样本：

因为它们产生的样本质量不如BS和DBS,无论是样本ROUGE的上界、均值和下界都较低。此外，nucleus sampling产生的样本有相当一部分是重复的。

评估和校准

使用生成模型G(ξ)生成的K个样本 Y1，Y2,...,Yk\ Y_1，Y_2,...,Y_k对在线模型M(θ)进行评估，使用ROUGE、BLUE或者BERTScore等评估方法，并对k个样本的质量进行从大到小的排序，于是使用以下损失函数来调整在线模型，以便它可以将具有高评价分数的样本排序得更高：

(1)LR(θ)=∑i<jmax(0,sθ(X,Y~j′ )−sθ(X,Y~i′ )+(j−i)∗λ)L^R(θ)=\sum_{i<j}max(0, s_θ(X, \tilde{Y}'^~_j ) − s_θ(X, \tilde{Y}'^~_i ) + (j − i) ∗ λ) \tag{1}

其中， sθ(X,Y~′ )\ s_θ(X, \tilde{Y}'^~) 是样本在在线模型M(θ)评估下的规范化的对数概率。  (j−i)∗λ\ (j-i)*λ 是样本  Y~j′ ,Y~i′ \ \tilde{Y}'^~_j ,\tilde{Y}'^~_i 动态的得分参数 ：

(2)sθ(X,Y~′ )=−1∣Y~′ ∣α∑t=1∣Y~′∣γtlog p(Y~′ ∣Y~′ <t,X;θ)s_θ(X, \tilde{Y}'^~)=-\frac{1}{|\tilde{Y}'^~|^\alpha}\sum_{t=1}^{|\tilde{Y}'|}γ_tlog\ p(\tilde{Y}'^~|\tilde{Y}'^~<t,X;\theta) \tag{2}

其中 α\ \alpha是一个超参数（类似于beam search中的长度惩罚）， γt\ γ_t 是常数位置权函数。

在模型的训练过程中，作者发现模型通常在后面的位置具有较低的词级的预测准确性，作者猜测可能是因为模型需要记忆更多的过程token来进行预测。为了让模型更加专注后面的位置，作者将 γt\ γ_t进行了改进：

(3)γt=γt~1∣Y~′ ∣∑i=1∣Y~′ ∣γt~=∣Y~′ ∣(∣Y~′ ∣+1−t)2∑i=1∣Y~′ ∣1i2γ_t=\frac{\tilde{γ_t}}{\frac{1}{|\tilde{Y}'^~|}\sum_{i=1}^{^{|\tilde{Y}'^~|}}\tilde{γ_t}}=\frac{|\tilde{Y}'^~|}{(|\tilde{Y}'^~|+1-t)^2\sum_{i=1}^{^{|\tilde{Y}'^~|}}\frac{1}{i^2}} \tag3

注意： 当MLE损失训练的模型的位置精度在后面的位置下降时，使用上述改进的加权函数。否则，仍然使用常数位置权函数 γt\ γ_t=1。

于是将对比损失函数与最大似然估计损失函数公式④进行联合得到最终的损失函数⑤：

(4)LMLE(θ)=−1∣Y∣log p(Y∣X;θ)L^{MLE}(θ)=-\frac{1}{|Y|}log\ p(Y|X;\theta) \tag4

(5)L(θ)=LR(θ)+βLMLE(θ)L(θ) = L^R(θ) + βL^{MLE}(θ) \tag 5

动量更新(Momentum Update)

由于beam search的不可微分性，通过公式⑤的损失函数只能优化在线模型M(θ)的参数，这样会导致模型在训练时收敛得很快

为了解决这一问题，作者对生成模型G(ξ)的参数的动量更新：

(6)ξ←mξ+(1−m)θξ ← mξ + (1 −m)θ \tag6

其中m是动量系数，反向传播时仅更新θ。作者提出当m = 0.99时生成模型G(ξ)有最大稳定性

实验结果

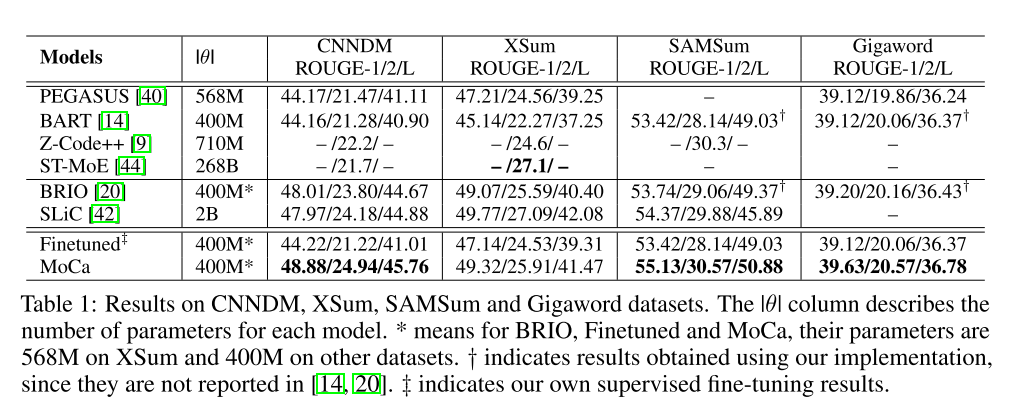
MoCa在CNNDM,SAMSum，Gigaword数据集均取得了SOTA的效果

总结

MoCa是一种用于文本生成的在线方法，目的是解决分配给候选样本的模型概率与其质量之间的差异。对于大型预训练transformers结构模型，MoCa在MLE损失方面始终优于普通微调。同时MoCa为beam search量身定制了评价函数。作者期望到将MoCa广泛应用到诸如机器翻译、跨语言文本摘要的多语言文本生成任务以及文本之外的生成任务。

参考文献

《Momentum Calibration for Text Generation》

属于 @威伦特 RSS