威伦特

在如今大模型时代，如果需要微调一个大模型无疑在时间和金钱方面的消耗是巨大的，而LoRA通过冻结了预训练的模型权重，并将可训练的秩分解矩阵注入到Transformer架构的每一层中，大大减少了下游任务的可训练参数的数量。尽管LoRA使得可训练参数更少，但是与微调效果相比结果相当甚至更好。

概述

自然语言处理中的许多应用程序依赖于将一种大规模的、预训练的语言模型应用于多个下游应用程序。这种适应通常是通过微调来完成的，它会更新预训练模型的所有参数。微调的主要缺点是新模型包含与原始模型一样多的参数。许多人试图通过仅调整一些参数或为新任务学习外部模块来缓解这种情况。这样，除了每个任务的预训练模型外，只需要存储和加载少量任务特定的参数，大大提高了部署时的运行效率。

然而，目前现有技术通常通过扩展模型深度或减少模型的可用序列长度来引入推理延迟，这些方法通常无法匹配微调基线，从而在效率和模型质量之间做出权衡。

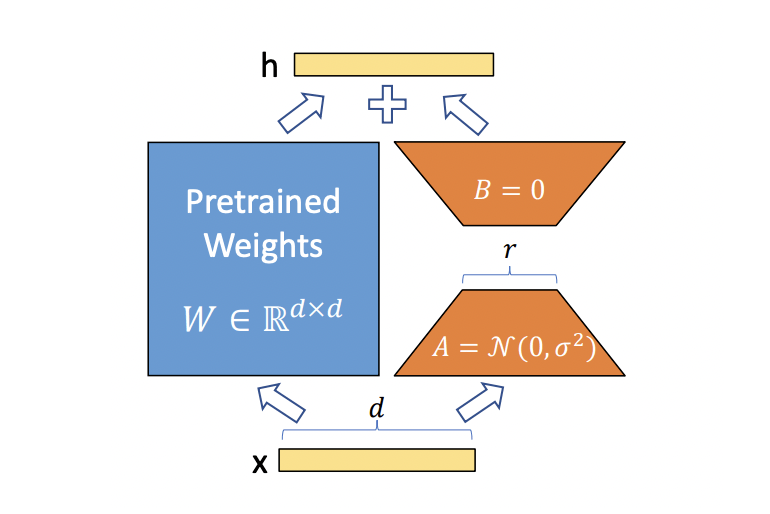
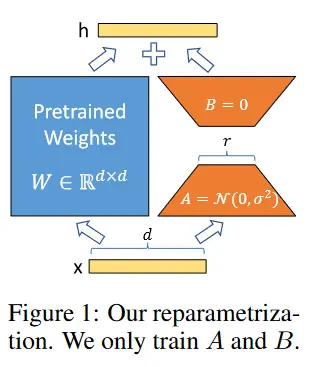
作者假设模型适应期间权重的变化也具有较低的“intrinsic rank”，从而导致作者能够提出的Low-Rank Adaptation(LoRA)方法。 LoRA允许通过优化自适应期间密集层变化的秩分解矩阵来间接训练神经网络中的一些密集层，同时保持预训练的权重冻结，如下图所示。

LoRA具有如下4个优点。

• （1）预训练模型可以共享并用于为不同任务构建许多小型LoRA模块。可以通过替换上图中的矩阵A和B来冻结共享模型并有效地切换任务，从而显着降低存储需求和任务切换开销。

• （2）当使用自适应优化器时，LoRA使训练更有效，并将进入硬件的门槛降低了多达3倍，因为作者不需要计算梯度或维护大多数参数的优化器状态。相反，作者只优化注入的、更小的低阶矩阵。

• （3）简单的线性设计允许在部署时将可训练矩阵与冻结权重合并，与完全微调的模型相比，不会引入推理延迟。

• （4）LoRA 与许多现有方法正交，可以与其中许多方法结合使用，例如prefix-tuning。

解释：研究人员将Transformer的输入和输出维度大小称为$d_{model}$。使用$W_q,W_k,W_v$和$W_o$来指代自注意力模块中的查询/key(键)/value(值)/output(输出)投影矩阵。 $W$ 指的是预训练的权重矩阵，而 $ΔW$指的是它在训练期间的累积梯度更新。使用 r 来表示 LoRA 模块的等级。

微调存在的问题

LoRA要解决的问题并不针对某一个特定的训练目标，不管你是情感分析，NER还是什么其他的，都可以使用它。它要解决的主要问题就是大语言模型在微调时候需要更新全部参数带来的效率和成本的上升。传统语言模型在做微调的时候是需要对全部参数进行更新的，假设原始大模型参数为 $Φ$ ，微调后我们需要将模型参数更新为 $Φ_0+ΔΦ$ 。当使用全量微调的时候，这两个参数的量级是一样的。这不仅给训练，也给部署带来了很大的挑战，因为这相当于你每个下游任务都要存储一份全量的参数。

$max\sum_{(x,y)∈Z}\sum_{t=1}^{|y|}log(P_Φ(y_t|x,y<t))$

其中，$Z = \lbrace(x_i, y_i)\rbrace i=1,..,N$,其中 $x_i$ 和 $y_i$ 都是text和target。

完全微调的一个主要缺点是，对于每个下游任务，作者学习一组不同的参数$ ΔΦ$，其维度$|ΔΦ|$等于$|Φ_0|$。因此，如果预训练模型很大（如今大模型参数都是上百亿），对微调模型的存储和部署变得非常困难。

于是作者采用了一种更有效的参数方法，其中任务特定的参数增量$ ΔΦ=ΔΦ(Θ)$ 由一组更小的参数$Θ$进一步编码,$|Θ|<|Φ_0|$。因此，寻找$∆Φ$的任务变成了对$Θ$进行优化：

$max\sum_{(x,y)∈Z}\sum_{t=1}^{|y|}log(P_{Φ_0}+ΔΦ(Θ)(y_t|x,y<t))$

作者建议使用低秩表示来编码$ΔΦ$，这既具有计算效率，又具有内存效率。可训练参数个数$|Θ|$可以小至$|Φ0|$的 0.01%。

方法

大型预训练模型中存在很多的密基层（dense layers），还有很多大矩阵的乘法运算。这些权重矩阵通常都是满秩的，作者发现这些模型通常都有更低的instrisic dimension，并且即使映射到一个更低维度上也可以有效的进行模型学习。其实说白了就是大模型在特定任务上微调的时候可能并不需要更新所有的参数，可能只需要部分参数就可以完成这个任务。

instrisic dimension:数据集中所包含的最少信息所需要的维度，也就是一个n维数据集最低可以用一个m维向量来表示（n>m）

instrisic rank:指能够用来描述数据集最重要信息的维度数

低秩参数更新矩阵

神经网络包含许多矩阵乘法的网络层。这些层中的权重矩阵通常具有满秩。在适应特定任务时，Aghajanyan等研究表明，预训练的语言模型具有较低的“instrisic dimension”，尽管随机投影到较小的子空间，但仍然可以有效地学习。受此启发，作者假设权重的更新在适应过程中也具有较低的“instrisic rank”。对于预训练的权重矩阵$W∈R^{d\times k}$，作者通过用低秩分解$W+ΔW$表示后者来约束其更新，其中$B∈R^{d\times r},A∈R^{r\times k}$并且$rank \ r<<min(d, k)$。在训练过程中，$W$被冻结，不接收梯度更新，而$A$和$B$包含可训练参数。请注意，$W$ 和$ΔW=BA$都与相同的输入相乘，并且它们各自的输出向量按坐标相加。对于 $ℎ=Wx$，作者修改后的前向传播产生：

$h=Wx+ΔWx=Wx+BAx$

上图中说明了重新参数化。对A使用随机高斯初始化，对B使用零初始化，因此$ΔW=BA$ 在训练开始时为零。然后作者用$a/r$缩放$ΔWx$ ，其中 $α$是$r$中的常数。当使用 Adam 进行优化时，如果作者适当地缩放初始化，调整$α$与调整学习率大致相同。因此，作者只是将$α$设置为作者尝试的第一个$r$，而不对其进行调整。当作者改变$r$时，这种缩放有助于减少重新调整超参数的需要。

LoRA不需要对权重矩阵进行累积梯度更新以在自适应期间具有满秩。LoRA 应用于所有权重矩阵并训练所有biases时，通过将LoRA rank r 设置为预训练权重矩阵的rank来粗略地恢复完全微调的表现力，随着作者增加可训练参数 3 的数量，训练 LoRA 大致收敛到训练原始模型.

将LoRA用于Transformer

将LoRA应用于神经网络中权重矩阵的任何子集，以减少可训练参数的数量。在 Transformer 架构中，self-attention 模块中有四个权重矩阵$W_q,W_k,W_v,W_o$，MLP模块中有两个。作者将$W_q,W_k,W_v$视为维度为$d_{model}\times d_{model}$ 的单个矩阵，即使输出维度通常被分割成注意力头。作者将研究限制为仅调整下游任务的注意力权重，并冻结 MLP 模块（不会在下游任务中接受训练）以实现简单性和参数效率。

LoRA也有其局限性。例如，如果选择将$A$和$B$吸收到$W$中以消除额外的推理延迟，则在单个前向传递中将输入批处理到具有不同$A$和$B$的不同任务这个过程并不简单。

实验结果

作者分别在Roberta large，GPT2/3等模型上进行了测试。分别对比了之前的几种少参数量微调方法。

文本理解任务

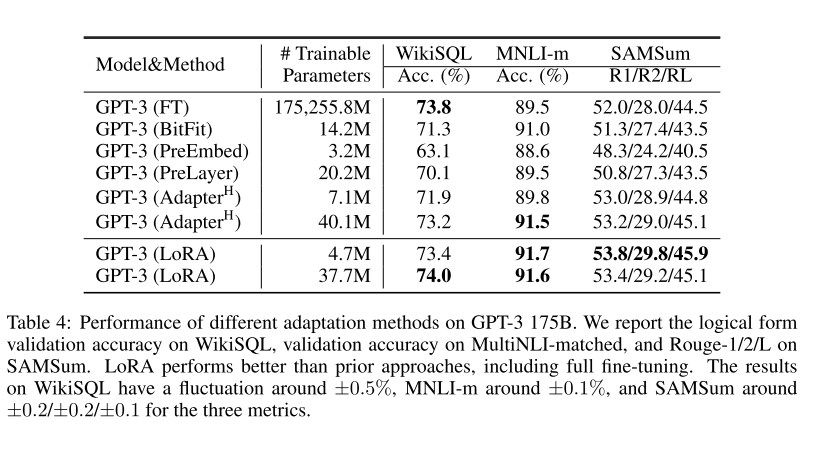
• 参数量：和现有参数高效微调方法持平或更低；
• 效果：优于其它参数高效微调方法，和全量微调基本持平甚至更高；
  

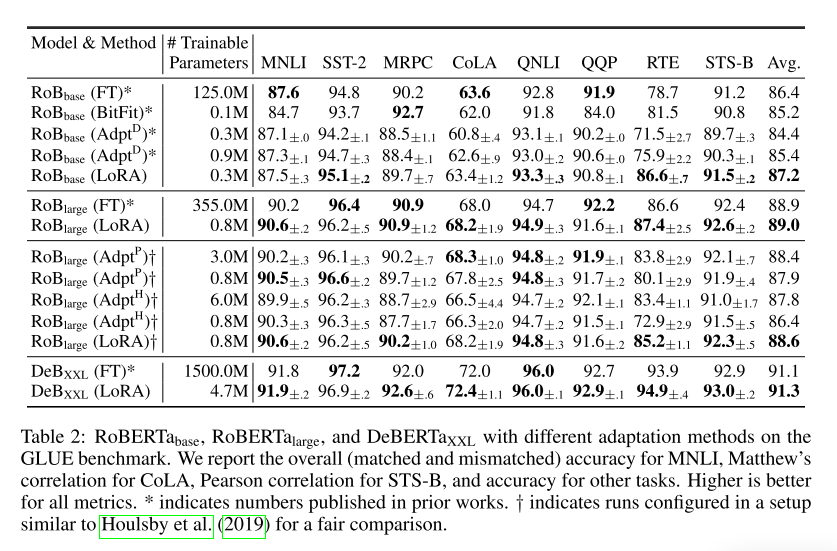
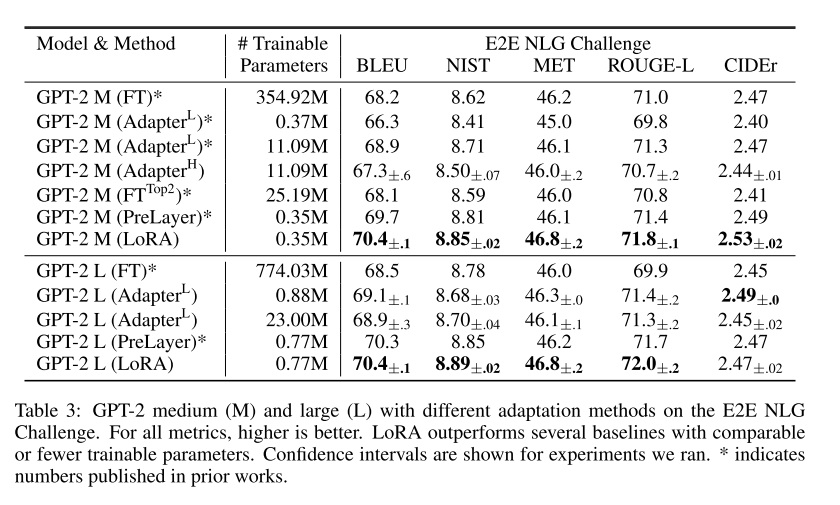
文本生成任务

生成任务上结论与理解任务类似，只不过在某些任务上Lora的优势可能没有那么明显或者略差。

可缩放性

• 增大参数量不会导致性能的不升反降；
• 性能上与全量微调持平或更好；

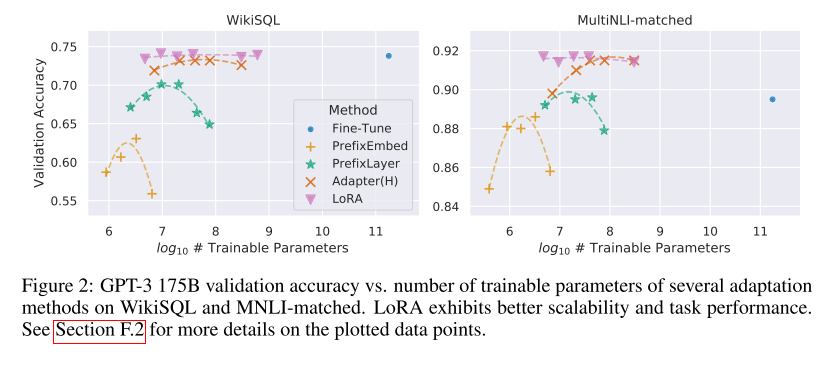
在Transformer中的应用

论文只研究了LoRA应用于transformer Attention层上的效果，发现同时对$W_q,W_k,W_v,W_o$应用LoRA效果较好。

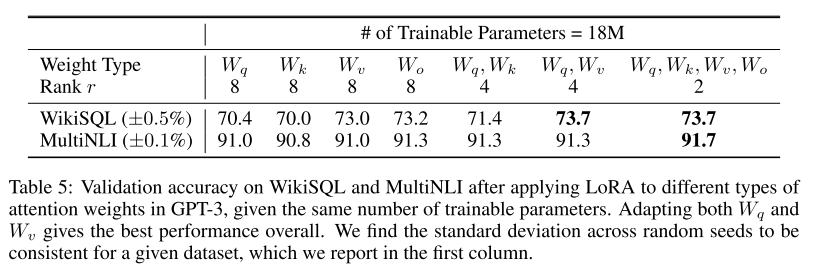
秩的选取

对于一般的任务，rank=1,2,4,8足矣，而对于一些领域差距比较大的任务可能需要更大的rank。

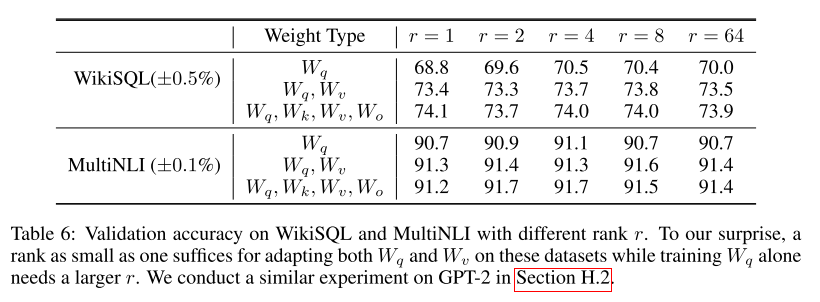
参考文献

[2106.09685] LoRA: Low-Rank Adaptation of Large Language Models (arxiv.org)

LoRA:大模型的低秩适配-最近大火的lora到底是什么东西？为啥stable diffusion和开源ChatGPT复现都在用？

[预训练模型之lora]《LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS》