在使用 RAG（Retrieval-Augmented Generation）时，我们通常需要在大量文本向量中，找到与查询最相似的若干条语句。最直观的方式是对所有向量逐一计算相似度（余弦相似度、欧氏距离等），然后进行比较。在数据规模较小时，这种方法尚可接受；但当数据量达到百万甚至更高量级时，逐一匹配将带来巨大的时间开销。

HNSW（Hierarchical Navigable Small World）正是针对这一问题提出的一种高效近似最近邻搜索方法。

概述

HNSW是一种用于高效搜索高维向量的数据结构，主要应用于近似最近邻（Approximate Nearest Neighbor, ANN）搜索场景。
它通过牺牲极少量精度，大幅降低在大规模数据集上进行相似度检索的计算成本。HNSW 将基于图的搜索方法与分层结构相结合，在搜索速度与准确率之间取得了良好的平衡，因此被广泛应用于推荐系统、图像检索、语义搜索以及自然语言处理等任务中。

为了更好地理解 HNSW 的设计思想，有必要先介绍对其影响最大的两种技术：跳表（Skip List） 和 NSW（Navigable Small World）图。

跳表

跳表在1990年由William Pugh提出，是一种基于概率的多层链表结构。在跳表中，每个节点不仅包含数据元素，还维护着指向不同层级后继节点的指针，用以加速查找过程。

跳表最底层（第 0 层）包含全部元素，结构等价于一个有序链表；而越往上层，节点数量越少，指针跨度越大。查询操作从高层开始，通过“跳跃”快速缩小搜索范围，再逐层向下逼近目标位置。由于跳表在保持链表插入效率的同时显著提升了查询性能，它被广泛应用于工程实践中，例如 Redis 的有序集合（ZSet）底层实现。

跳表的查询过程如下所示：查询从最高层开始，如果发现当前节点中的元素大于查询的目标值，那么就会回退一个节点，并在这个节点的下一层进行查询，一直重复这个过程，直到查询到目标值，如下图所示。

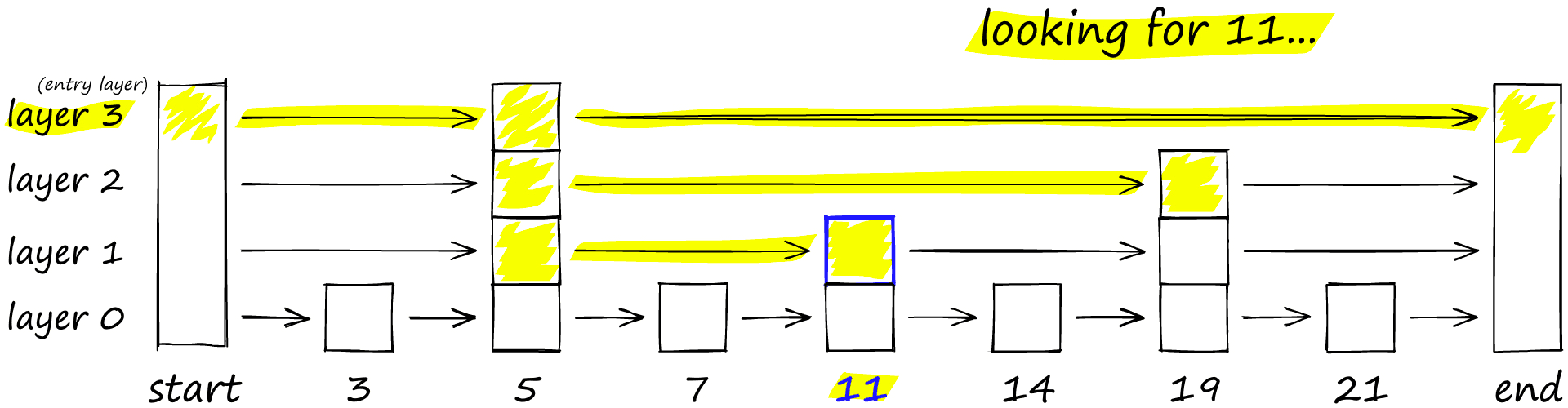
HNSW继承了跳表分层的思想，高层具有较长的边（用于快速搜索），低层具有较短的边（用于精确搜索）。

Navigable Small World Graphs(NSW)

NSW图是在 2011–2014 年间提出的一类基于图的近邻搜索结构。其核心思想是构建一个近邻图，使节点同时拥有长距离边和短距离边，从而在搜索过程中既能快速跳转，又能逐步逼近目标，从而提高查询效率。

NSW图中每个顶点都与若干个其他顶点相连。称这些相连的顶点为“friends”，每个顶点都会维护一个friend list，所有节点及其连接关系共同构成了搜索图。

查询时，需要指定一个入口点（entry point），从该节点出发，采用贪心策略不断移动到与查询向量距离更近的相邻节点，样一直迭代。当无法找到更近的邻居时，搜索停止。具体如下所示。

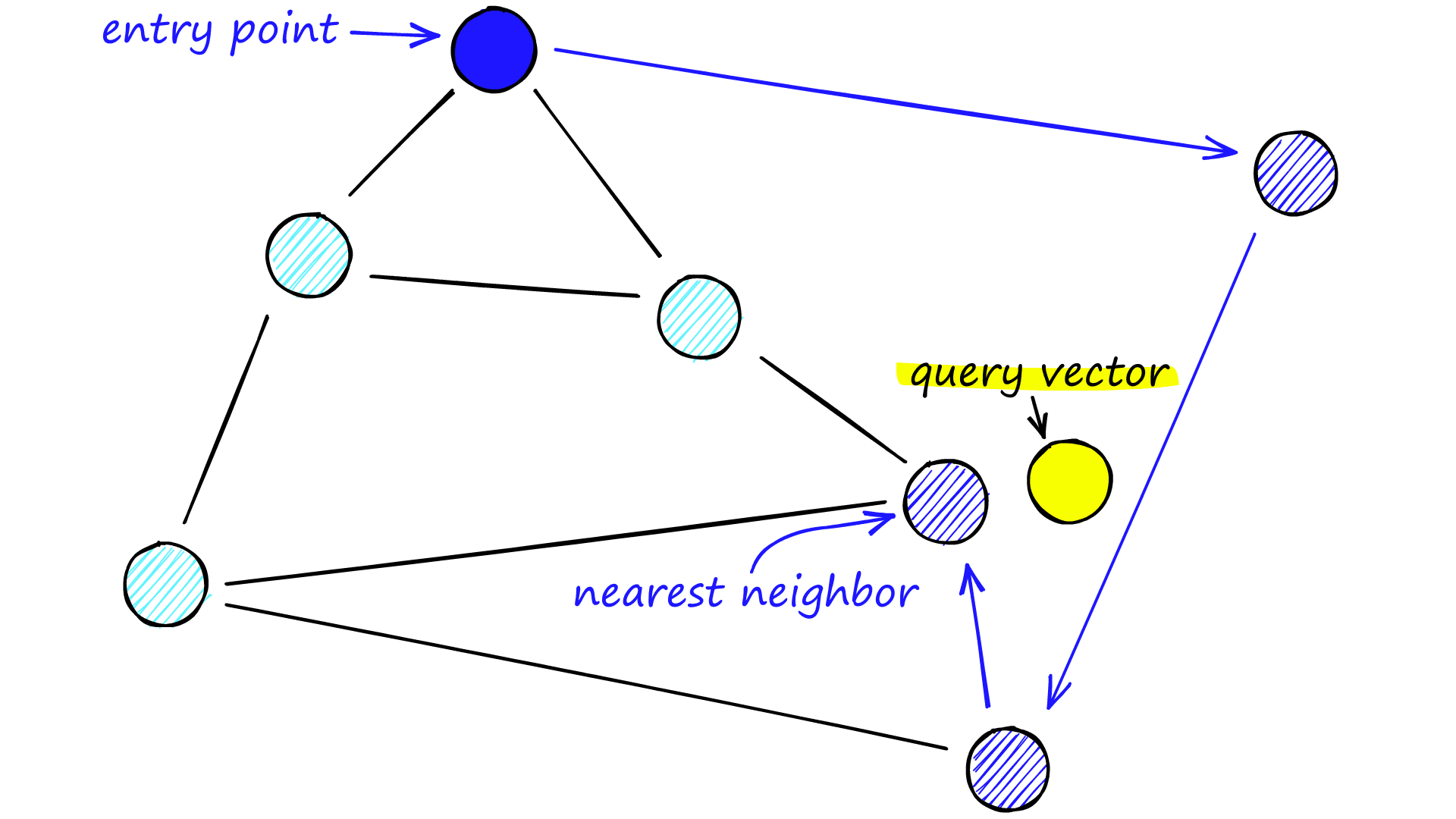
然而NSW通过贪婪算法专注于找到局部最优，当找不到更近的顶点的时候便退出。而在图中节点度数较少的时候，搜索过程容易陷入局部最小值，从而过早终止。

为缓解这一问题，常见的改进思路包括：

• 提高节点的平均度数，以增强图的连通性（但会增加内存和搜索成本）
• 从高度数节点开始搜索，以提升搜索的全局性（这正是 HNSW 的关键设计之一）

度数即图中与节点直接相连的边数

HNSW

HNSW是对NSW自然的改进，同时也借鉴了跳表中分层搜索的思想。

在 HNSW 中：

• 顶层节点数量最少，连接距离最长
• 底层包含全部节点，连接距离最短
• 搜索从顶层开始，逐层向下进行

这种结构使得搜索过程能够先快速定位到“可能正确的区域”，再在底层完成精确搜索。

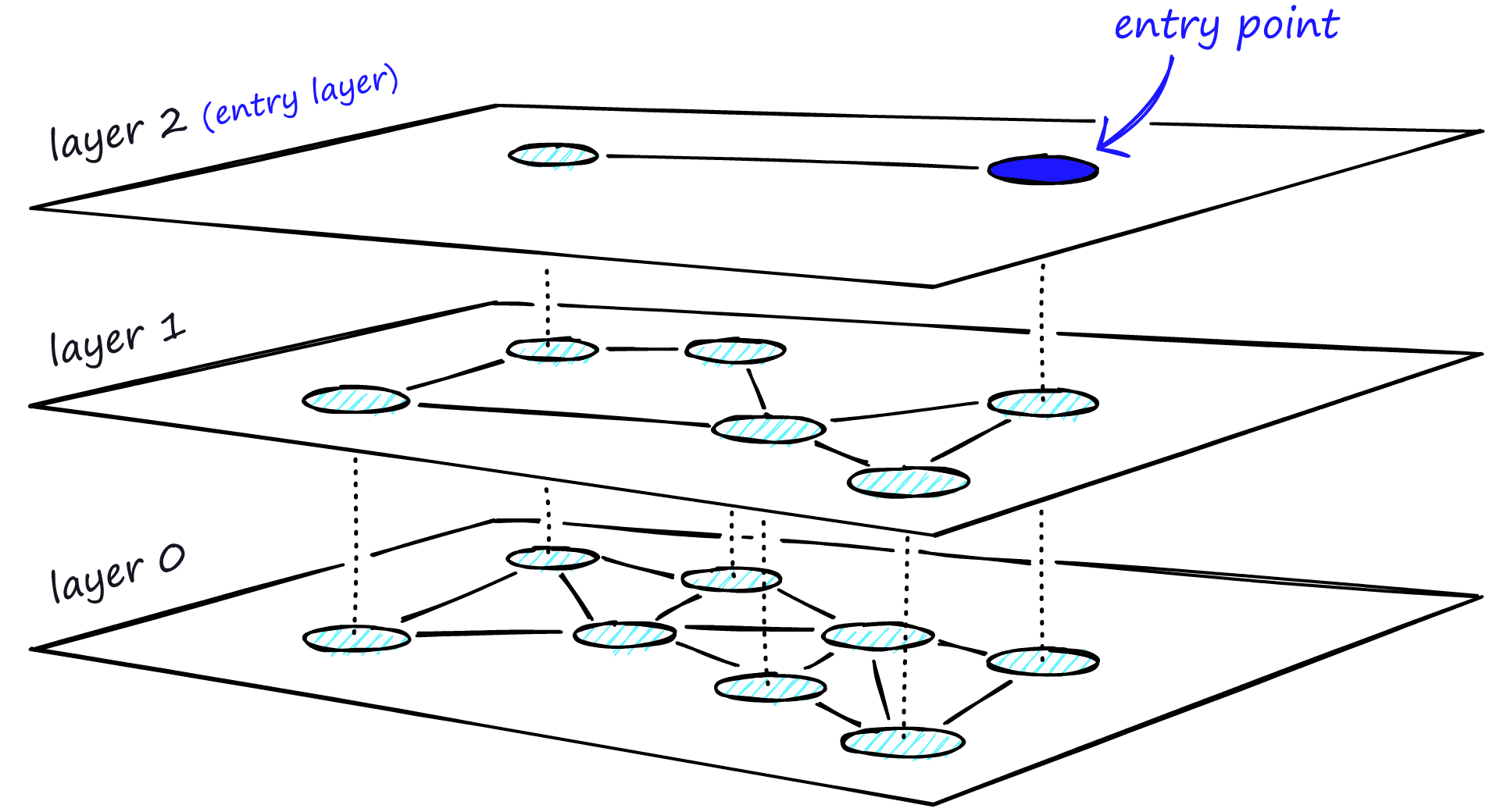
HNSW搜索过程

在搜索阶段，HNSW 使用参数$ef_{search}$，表示搜索过程中允许维护的候选节点数量上限。

搜索流程如下：

• 从最高层的入口点开始搜索

• 在除第 0 层外的各层，采用宽度为 1 的贪心搜索，逐层向下定位搜索区域

• 进入第 0 层后，以$ef_{search}$为宽度执行局部图搜索

• 最终从候选集合中返回距离查询向量最近的 K 个节点作为检索结果

整个查找过程如下图所示：

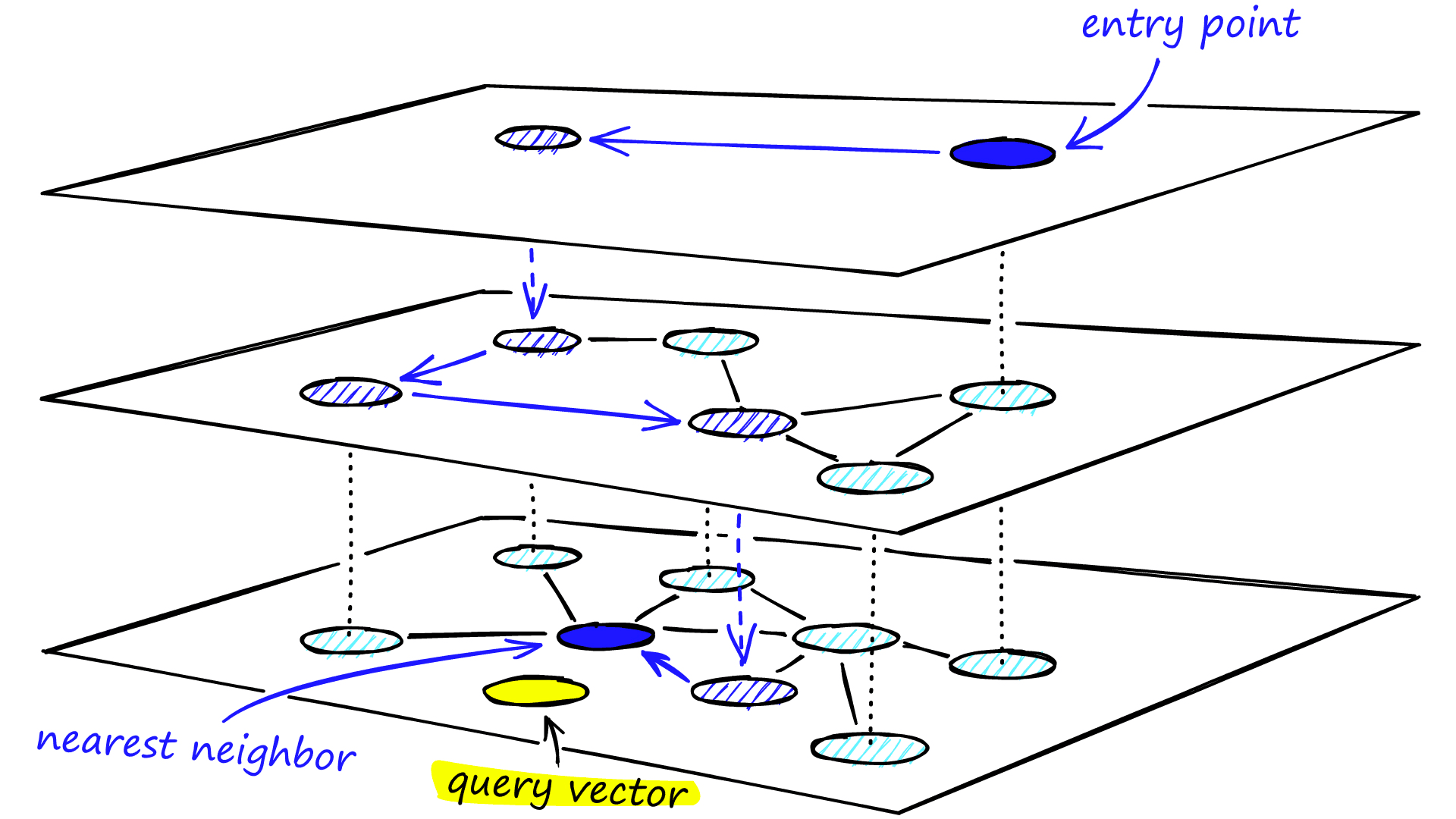
HNSW的构建过程

确定层数和层中节点数

由于HNSW是一种多层索引结构，所以构建HNSW的第一步就是确定层数和每一层所含有的节点个数。

而这两个的确定都与$m_L$层级乘数这个参数有关，具体计算方法如下：

层数确定：

总层数 $Level$ 的计算公式为：

$Level=\lfloor \frac{-log(N)}{log(m_L)}\rfloor$

其中$N$为总节点的个数。

节点层级分配：

在确定了层数后，需要为每个节点分配其所属的层级。算法依次从底层（第0层）开始向上判断，具体步骤为：

1. 为每个节点生成一个随机数 $rand \in (0, 1)$。
2. 从第0层开始逐层计算累计概率阈值：
   • 若 $rand > P[0]$，则该节点可进入第1层；
   • 若继续满足 $rand > P[1] + P[0]$，则可继续升至更高层，依此类推。
3. 节点最终停留的层级 $n$ 满足条件：

$rand \le \sum^n_{k=0}P[N]$

​ 即节点将分布于第0层至第$n$层。

其中，节点出现在第 $N$ 层的概率 $P[N]$ 由下式给出：

$P[N]=func(level=N,m_L)\\=(m_L)^{M}*(1-m_L)$

整个构建过程如下图所示：

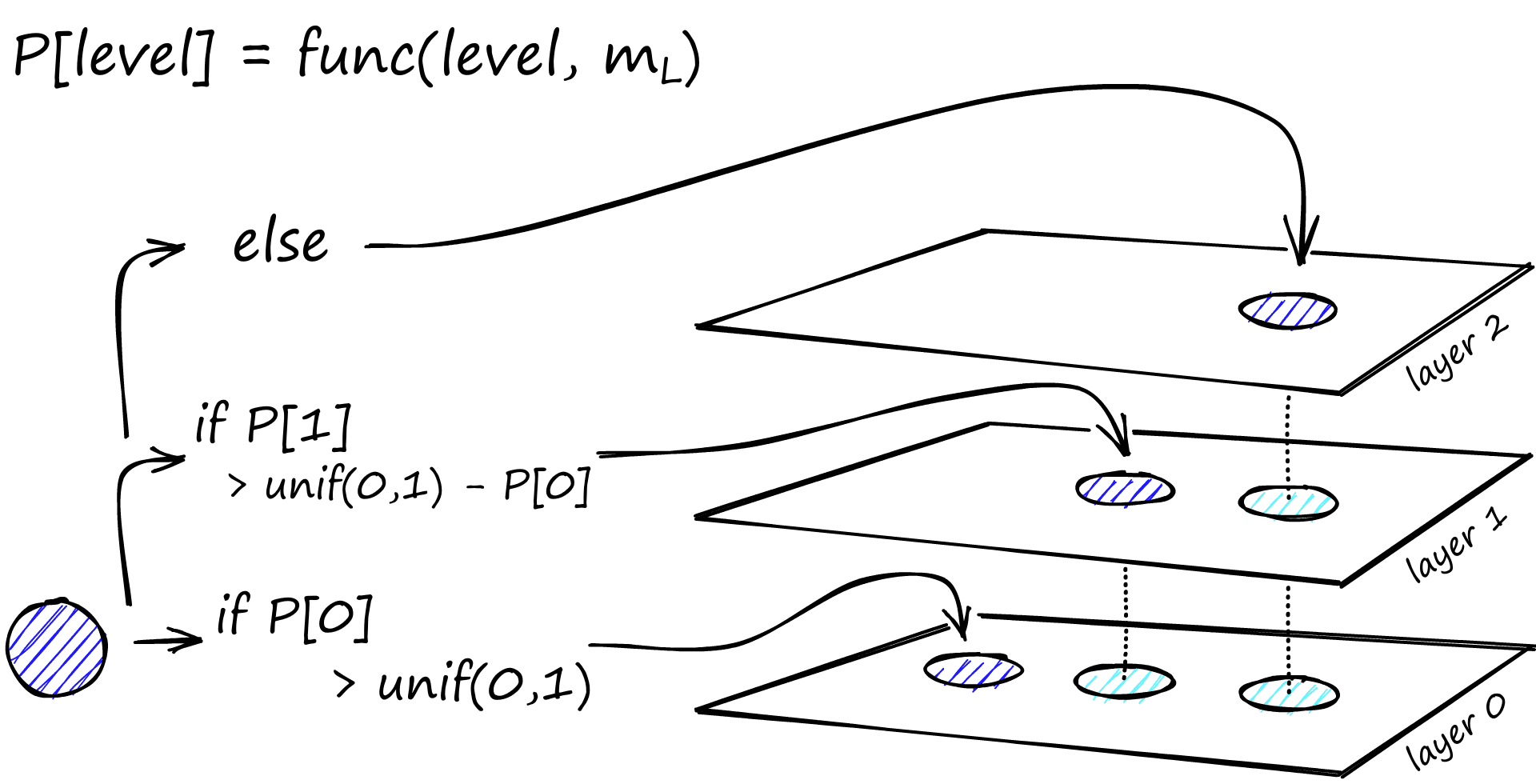
$m_L$通常设为$1/ln(M)$，其中$M$为节点除第0层外的最大度数

确定节点的连接关系

在确定层数与各层节点数量之后，最后一步是进行连边，即按照特定规则将每层中的节点连接起来。

连接过程需要设定两个重要参数：

• 每层节点最大度数 $M$
• 连接候选节点数 $ef$（该参数是一种优化手段，通过限制每层参与连边筛选的候选节点数量，以提升构建效率）

连接过程采用自顶向下的方式进行。以节点 $q$ 的连接为例：

1. 从顶层开始，采用贪心搜索算法（此时 $ef = 1$）找到当前层与 $q$ 最接近的节点；
2. 进入 $q$ 实际所在的层级后，将 $ef$ 恢复为预设值，找出该层中距离 $q$ 最近的 $ef$ 个候选节点；
3. 从中选择距离最近的 $M$ 个节点尝试建立连接。

但在连接至某个已有节点 $v$ 时，需判断其邻居数是否已达上限：

• 如果 v 的当前邻居数 $≤ M$：直接加边
• 如果 v 的邻居数 $> M$：那么会触发剪枝

剪枝过程并非简单保留最近邻、移除较远节点，而是采用一种称为启发式邻居选择的算法，旨在保留那些彼此距离相对较远、但均靠近 $q$ 的邻居节点。相关实现可参考 hnswlib启发式邻居选择源码：

 void getNeighborsByHeuristic2(
        std::priority_queue<std::pair<dist_t, tableint>, std::vector<std::pair<dist_t, tableint>>, CompareByFirst> &top_candidates,
        const size_t M) {
        if (top_candidates.size() < M) {
            return;
        }

        std::priority_queue<std::pair<dist_t, tableint>> queue_closest;
        std::vector<std::pair<dist_t, tableint>> return_list;
        while (top_candidates.size() > 0) {
            queue_closest.emplace(-top_candidates.top().first, top_candidates.top().second);
            top_candidates.pop();
        }

        while (queue_closest.size()) {
            if (return_list.size() >= M)
                break;
            std::pair<dist_t, tableint> curent_pair = queue_closest.top();
            dist_t dist_to_query = -curent_pair.first;
            queue_closest.pop();
            bool good = true;

            for (std::pair<dist_t, tableint> second_pair : return_list) {
                dist_t curdist =
                        fstdistfunc_(getDataByInternalId(second_pair.second),
                                        getDataByInternalId(curent_pair.second),
                                        dist_func_param_);
                if (curdist < dist_to_query) {
                    good = false;
                    break;
                }
            }
            if (good) {
                return_list.push_back(curent_pair);
            }
        }

        for (std::pair<dist_t, tableint> curent_pair : return_list) {
            top_candidates.emplace(-curent_pair.first, curent_pair.second);
        }
    }

太长不看版：

输入：top_candidates（候选邻居，按离q的距离排序）
目标：选出 ≤ M 个邻居

1. 若候选数 < M，直接返回
2. 按与 q 的距离从近到远排序
3. 依次尝试加入候选点 u
4. 若 u 被已选邻居“遮挡”，丢弃
5. 否则保留
6. 返回最终邻居集合
例子：如果 A→B 是已选边，并且 B→C 的距离小于 A→C 的距离，那么 A→C 会在启发式邻居选择中被减枝。

同时，这些已连接的点将作为下一层搜索的入口节点，该过程逐层向下迭代，直至达到最底层。在最底层中，每个节点的连接数量上限由参数 $M_{\text{max}}$ 控制，通常设置为 $M_{\text{max}} = 2M$。

上述连接操作将对图中的每个节点依次执行，最终完成整个多层图结构的构建。

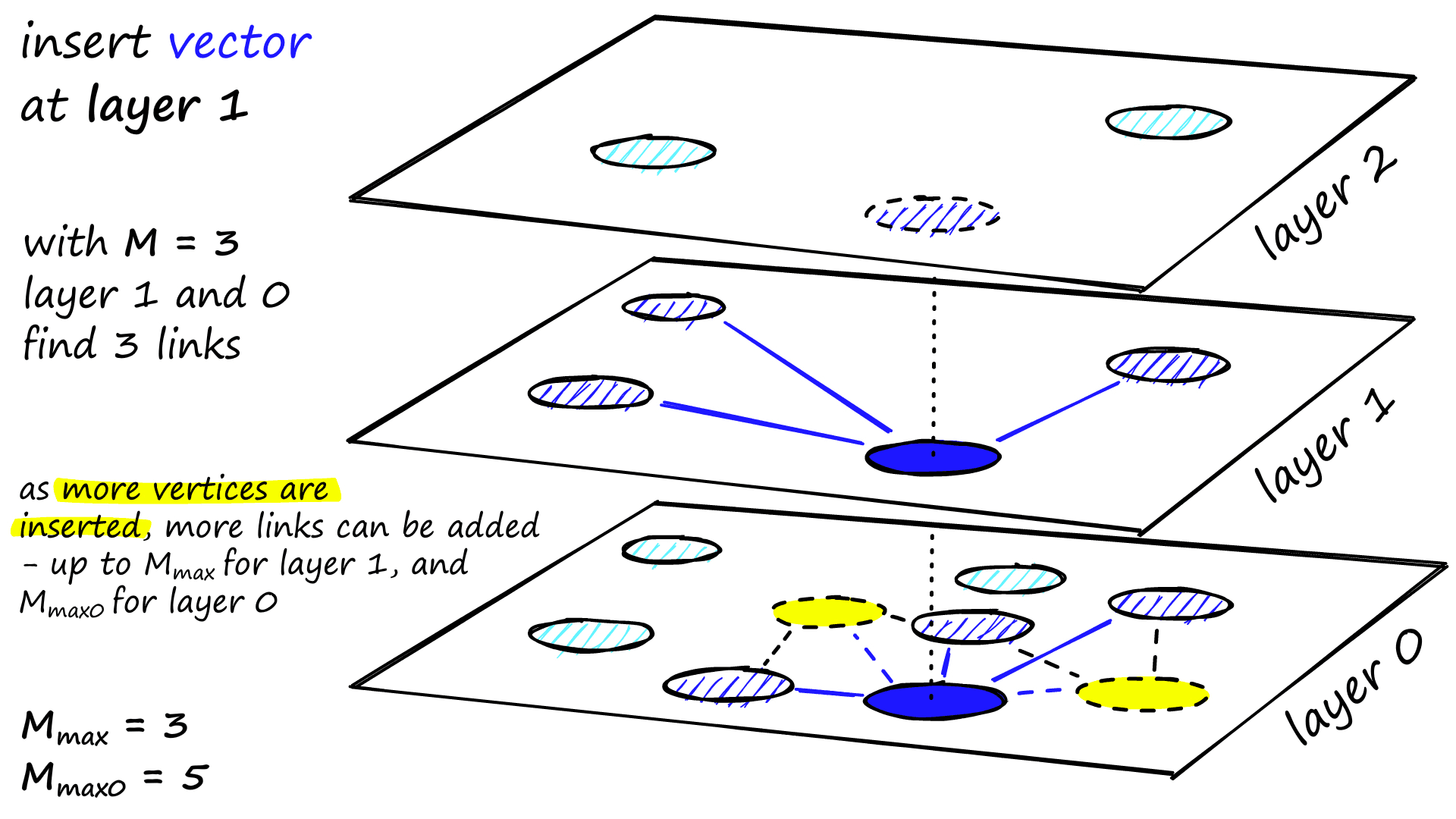
以上便完成了 HNSW 索引的构建过程。可以看到，整个构建过程中需要主动设置的参数实际只有两个：$M$（每层最大连接数）与 $ef$（构建时的候选节点数）。

而在搜索阶段，我们需要设置的参数为 $ef_{search}$（搜索时的候选队列大小）。

那么，在实际项目中应如何合理配置这三个参数呢？

参数的设置

使用 Sift1M 数据集对上述参数设置进行验证，实验结果如下：

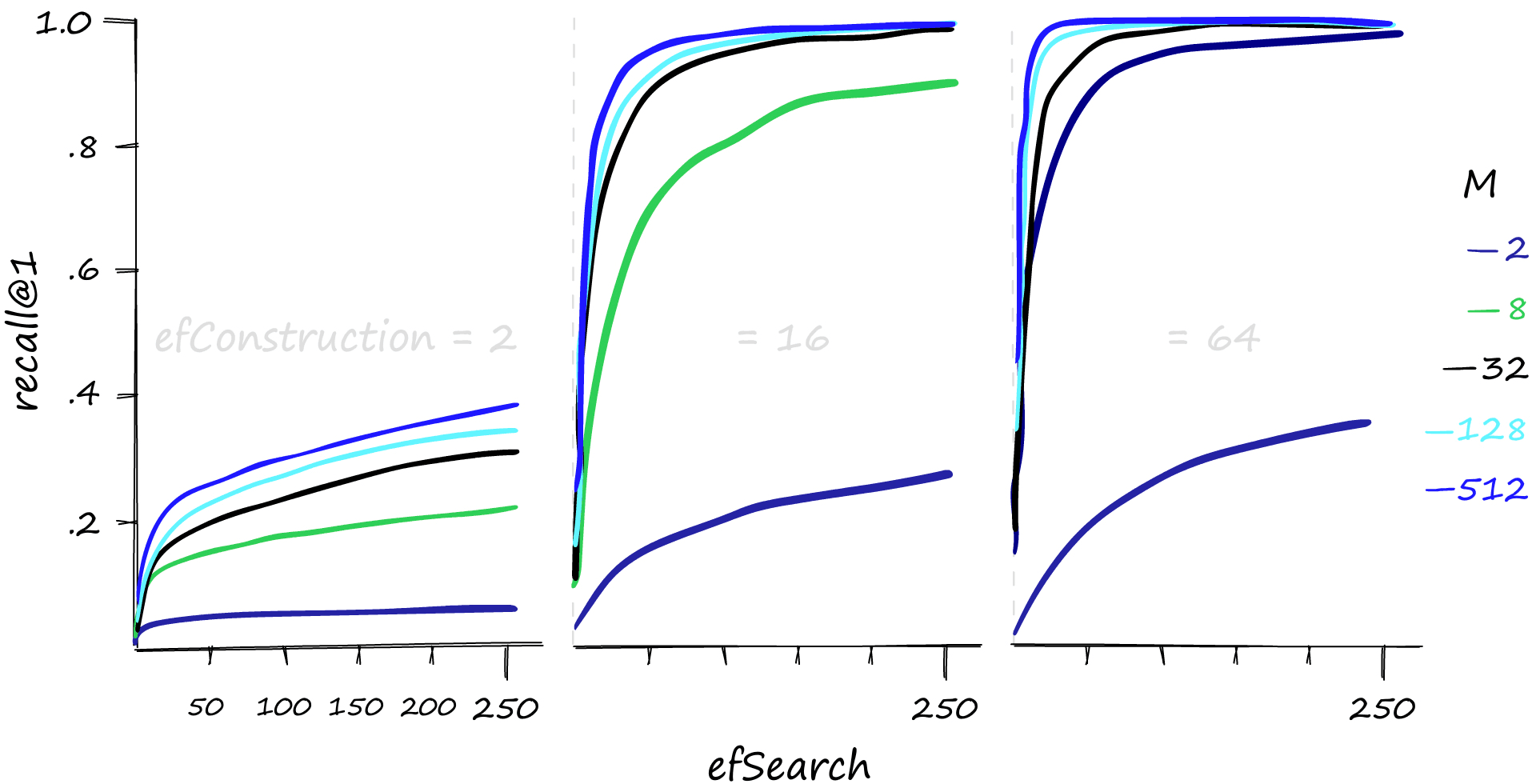
$M$、$ef$（即 $efConstruction$）和 $ef_{search}$ 的值越高，通常越能提升查询的准确率——但需要注意的是，提升效果存在合理区间，并非参数越大性能就会持续提升。

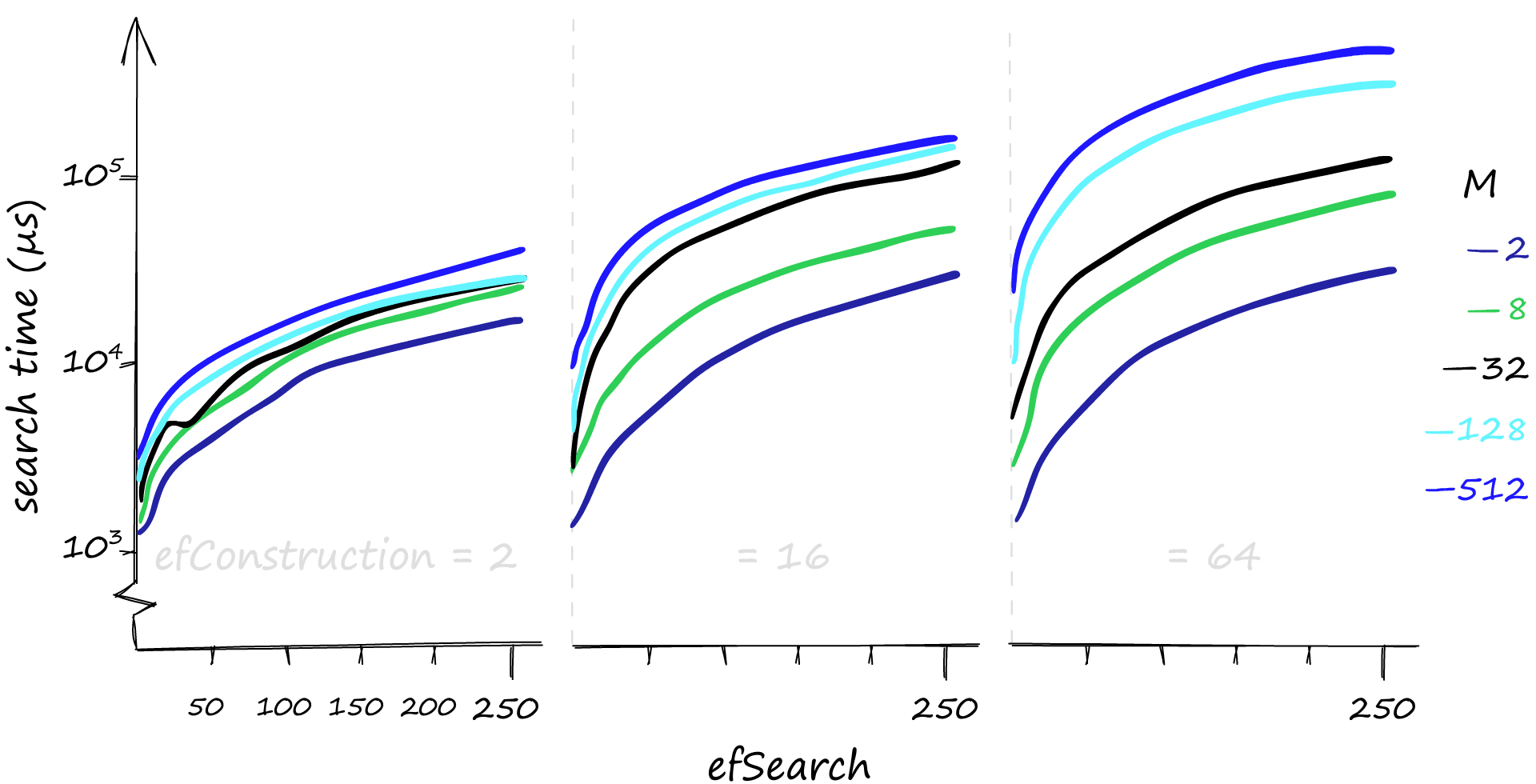
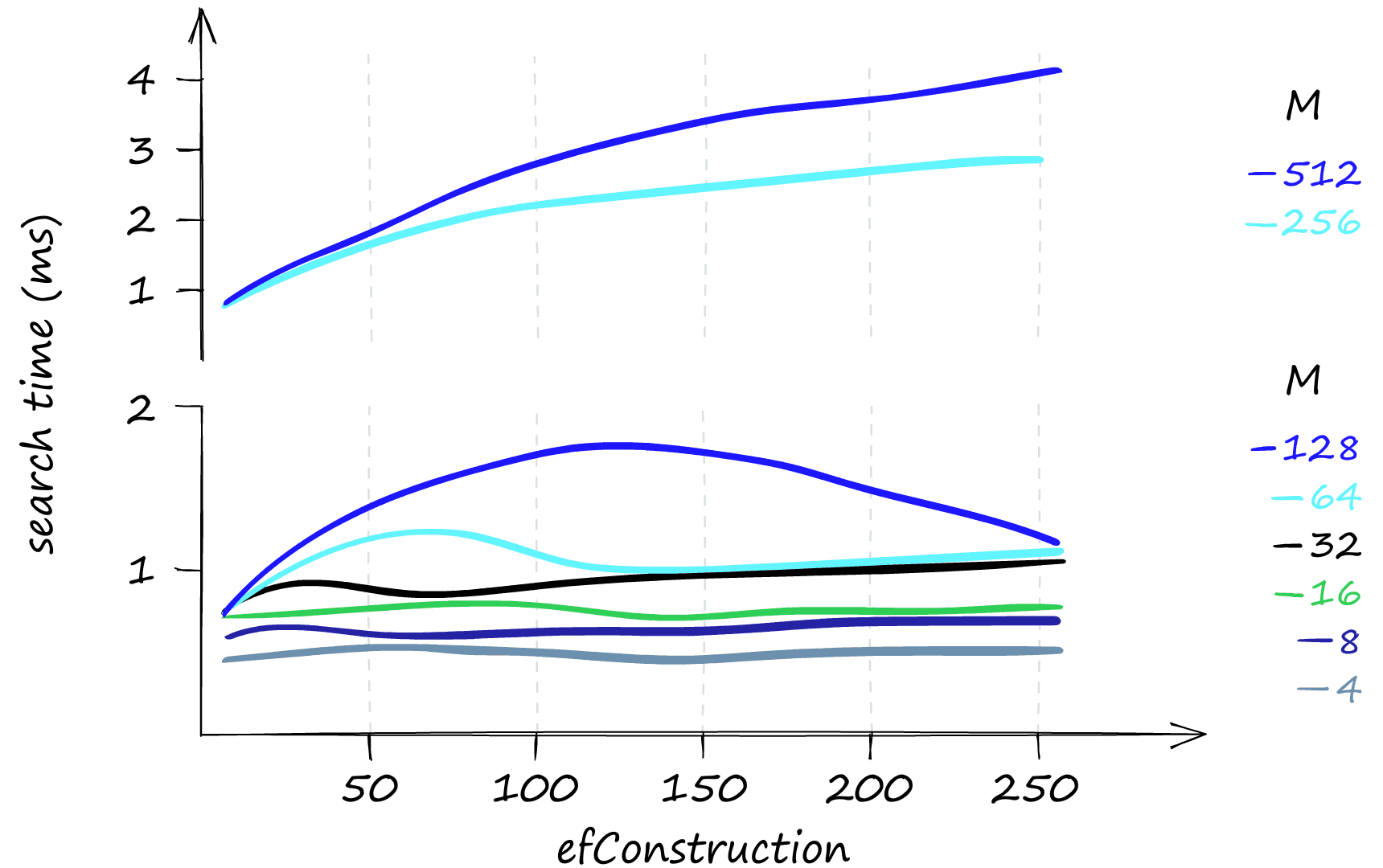
提高 $M$、$ef$ 和 $ef_{search}$ 的参数值，尤其在高并发查询场景下，会显著增加检索耗时。

若查询以低并发为主，则提升 $ef$ 参数是最佳选择。该参数能在几乎不影响检索耗时的情况下提高准确率，尤其是在搭配较低的 $M$ 值时效果更为明显。同时，$ef$ 对单次查询的耗时影响甚微，尤其是在 $M$ 值较低的情况下，检索时间几乎不受 $ef$ 变化的影响。

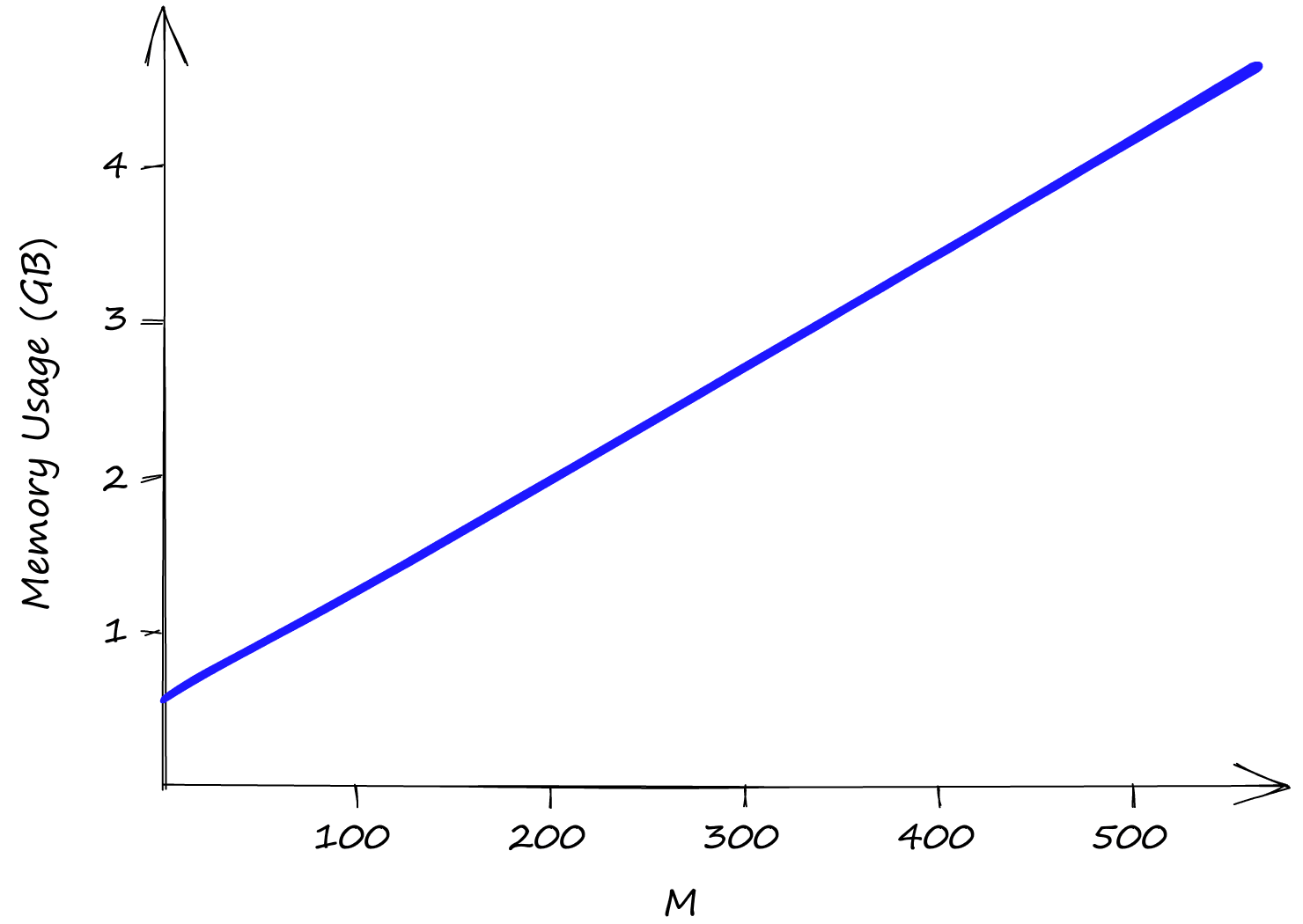
$ef$ 与 $ef_{search}$ 参数均不影响索引内存使用量，内存消耗完全由 $M$ 参数决定。即使将 $M$ 设为较低值 2，索引大小也已超过 0.5GB；而当 $M$ 值提升至 512 时，索引容量将接近 5GB。

总结

HNSW 在搜索性能方面表现卓越，但其高内存消耗也意味着更高的基础设施成本。在内存受限的场景中，可以结合 PQ（Product Quantization） 或 IVF 等技术进行折中优化。

参考文章

[1] Hierarchical Navigable Small Worlds (HNSW) | Pinecone

[2] Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs