感知机算法

感知机是由美国学者Fran Rosenblatt 在1957 年提出来的一种算法,也是作为神经网络（深度学习）的起源的算法。

分类(classification)指的是预测样本所属类别的一类问题。形式化表述，分类问题的目标就是给定输人样本x，将其分配给K种类别中的一种，其中k=1,…,K。如果K=2，则称为二分类，否则称为多分类。

线性分类模型与感知机算法

线性分类模型就是通过一条“线”将数据一分为二。线性模型由特征函数和对应的权重向量组成。

而通过线性分类模型进行分类的话，必须先将样本转化为向量然后有一个感知机分类器才能进行。

特征向量与样本空间

特征向量：描述样本特征的向量。

样本空间：样本分布的空间。

在收集了大量的样本后，可能会得到一个密集的样本空间。

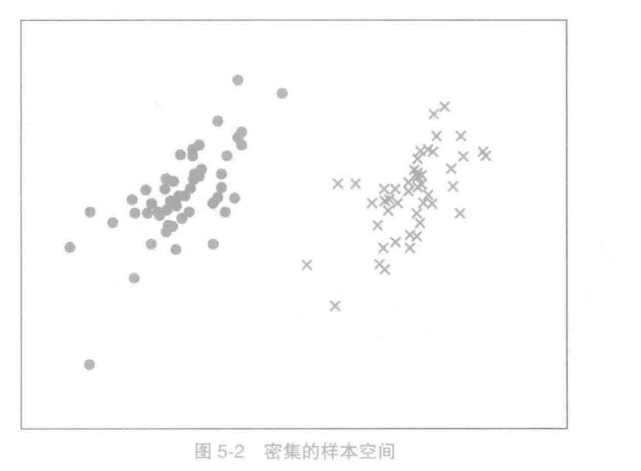
在样本转化为了特征向量后，分类问题实质上就是对样本空间的切割问题。

决策边界与分离超平面

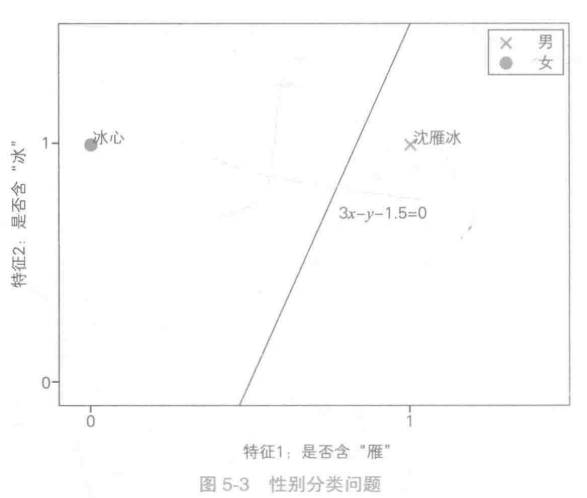
如上图所示，若两个样本可以通过一条直线分开。那么左右两边称为决策区域，而这条直线成为了决策边界。

二维空间中，如果决策边界是直线，则称产生该决策边界的模型为线性分类模型。

三维空间中的线性模型用平面做决策，任意维度空间中的线性决策边界统称为分离超平面。

二维空间中的直线方程:w_1x+w_2y+b=0, \\将其推广到N维空间:w_1x+w_2y+w_3z+.....+b=0 \\其中，w_1,w_2...,w_N是权重，b为截距，将b看为权重后，在特征向量的尾部添加一个1，即：\\ w=[w_1,....,w_N,b],x=[x,y,z,....,1]

如上图：直线方程为3x-y-1.5=0,那么权重向量为【3,-1,-1.5】,那么“沈雁冰”的特征向量为【1，1，1】

在有了决策边界的方程之后，线性模型使用方程左边的符号来作为最终的决策。

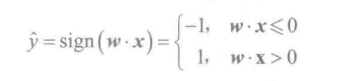
例如：

沈冰雁【1，1，1】带入直线方程3-1-1.5=0.5>0，决策符号为1。

线性可分：如果数据集中所有样本都可以被分离超平面分割。

若出现线性不可分的数据，我们可以采用如下方式来进行分类：

定义更多的特征
将数据映射到高维度

给定了训练集，可以通过感知机来进行训练线性模型。

读入训练样本，进行预测singn(w • X)
计算与正确答案的误差，根据误差进行调参

利用二维平面例子来进行解释，

第一种情况是错误地将正样本（y=1）分类为负样本（y=-1）。此时，wx<0，即w与x的夹角大于90度，分类线 l 的两侧。修正的方法是让夹角变小，修正w值，使二者位于直线同侧：

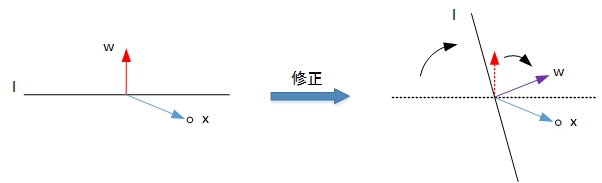
第二种情况是错误地将负样本（y=-1）分类为正样本（y=1）。此时，wx>0，即w与x的夹角小于90度，分类线 l 的同一侧。修正的方法是让夹角变大，修正w值，使二者位于直线两侧：

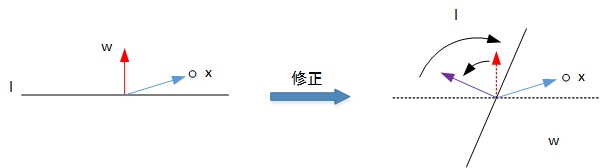
经过两种情况分析，我们发现每次w的更新表达式都是一样的：w:=w+yx。掌握了每次w的优化表达式，那么就能不断地将所有错误的分类样本纠正并分类正确。

例如：

在x=-0.3，y=0.96的时候 不符合，此时更新w和b， \\w_1=w_1+z*x*ŋ=1-0.3*0.5=0.85，\\w_2=w_2+z*y*ŋ=1+0.96*0.5=1.48\\ b=b+1*ŋ=-0.5

将更新后的w，b带入迭代，由于此时数据比较好，均通过了训练，迭代结束。

代码实现

import numpy as np
import matplotlib.pyplot as plt
# 初始化 w 和 b
w,b = np.array([0, 0]),0 
# 向量的点积
def d(x):
    return np.dot(w,x)+b 
#构造数据
X = np.array([[5,2], [3,2], [2,7], [1,4], [6,1], [4,5]])
Y = np.array([-1, -1, 1, 1, -1, 1])
run = True
while run:#迭代
    run = False
    for x,y in zip(X,Y):
        if y*d(x)<=0:
            w,b = w+y*x,y+b
            run = True
            break
print(w,b)
positive = [x for x,y in zip(X,Y) if y==1]
negative = [x for x,y in zip(X,Y) if y==-1]
line = [(-w[0]*x-b)/w[1] for x in [-100,100]]
plt.title('w='+str(w)+', b='+str(b))
plt.scatter([x[0] for x in positive],[x[1] for x in positive],c='green',marker='o')
plt.scatter([x[0] for x in negative],[x[1] for x in negative],c='red',marker='x')
plt.plot([-100,100],line,c='black')
plt.xlim(min([x[0] for x in X])-1,max([x[0] for x in X])+1)
plt.ylim(min([x[1] for x in X])-1,max([x[1] for x in X])+1)
plt.show()

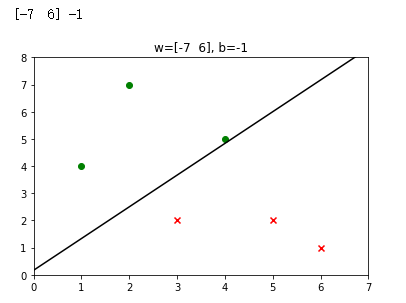
为了深刻地理解感知机算法原理,则必须了解损失函数等概念。

损失函数与随机梯度下降

在有监督的机器学习算法中，我们希望在训练过程中最小化每个训练样例的误差。这是使用梯度下降等一些优化策略完成的。而这个误差来自损失函数。

损失函数就是来衡量模型在训练集上的错误程度

学习率：对特征向量w，带入损失函数中,称为J(w)，对J(w)求导，齐反方向为损失函数减少速度最快的方向。如果该点反方向移动会使损失函数减少，即w=w-a△w，a为[0，1)常数，则a为学习率。

随机梯度下降：每次迭代随机选取部分样本，计算损失函数的梯度，让参数反方向移动。

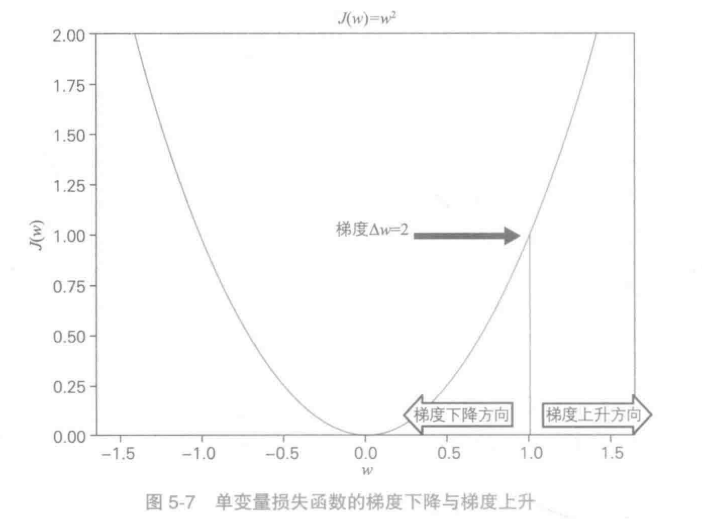
eg：假设损失函数J(w)=w^2,w=1时， △w=2w=2,方向为正无穷\\ 如果参数反方向移动，取学习率a=0.5，\\ 则w\leftarrow 1-0.5*2=0,则J(0)=0,马上就减少了

在多维度函数中，一直迭代梯度下降，最终会使损失函数到达底部，函数的最小值。

具体到线性模型中来，感知机的损失函数为错误分类点到超平面的距离：

J(w)=\frac{1}{N}\sum^{N}_{i=1}max(0,-y*w*x) \\其中，y为误分类点，w为参数，x为训练样本自变量

投票感知机和平均感知机

假设有10 000个实例，模型在前9999个实例的学习中都完美地得到正确答案，说明此时的模型接近完美了。可是最后一个实例是个噪声点,朴素感知机模型预测错误后直接修改了模型，导致前面9999个实例预测错误，模型训练前功尽弃。怎么办呢?

可以采用简单的解决方法：投票感知机和平均感知机

投票感知机：在每次迭代的时候，将参数、准确率都保留。在最后预测的时候每个模型都给出自己的结果，然后乘上对应的准确率加权平均值就得出最终结果。最后结果最高的确立为最终的参数。

平均感知机：对每次迭代取模型参数加权相加平均，将平均值作为最终结果。

实例

通过使用hanlp来对"赵建军", "沈雁冰", "陆雪琪", "李冰冰"进行性别的分类

from pyhanlp import *
from tests.test_utility import ensure_data
PerceptronNameGenderClassifier = JClass('com.hankcs.hanlp.model.perceptron.PerceptronNameGenderClassifier')#模型提取
TRAINING_SET = os.path.join('./train.csv')
TESTING_SET = os.path.join('./test.csv')
def run_classifier():
    classifier = PerceptronNameGenderClassifier()
    print('训练集准确率：', classifier.train(TRAINING_SET, 10, False))
    model = classifier.getModel()
    print('特征数量：', len(model.parameter))
    test="赵建军", "沈雁冰", "陆雪琪", "李冰冰"
    for name in test:
        print('%s=%s' % (name, classifier.predict(name)))#进行预测
    print('测试集准确率：', classifier.evaluate(TESTING_SET))
if __name__ == '__main__':
    run_classifier()

训练集准确率： P=85.72 R=85.05 F1=85.39
特征数量： 9089
赵建军=男
沈雁冰=男
陆雪琪=女
李冰冰=女
测试集准确率： P=83.35 R=82.82 F1=83.09

总结

感知机模型简单、易学习，是基本的机器学习模型，很多机器学习模型是在感知机模型的基础上变化扩展而得到的。
感知机模型由于其简单，在应用时也有一定的局限，主要体现在以下几点。

感知机只能处理线性可分的数据集，线性不可分的数据集会引起分离超平面的震荡而无法收敛。
感知机是误分类驱动的模型，模型的解不唯一。离群点对结果影响很大。
感知机的判别模型由符号函数给出，无法表示更复杂的非线性映射。

威伦特