威伦特

动态规划 dp

根据数组的长度 num.size() 判断数组是否可以被划分。如果 n%2!=0，则不可能将数组分割成元素和相等的两个子集，因此直接返回 false。

计算整个数组的元素和 sum 以及最大元素maxNum。如果 sum 是奇数，则不可能将数组分割成元素和相等的两个子集，因此直接返回false。如果 sum 是偶数，则令 target= sum/2,如果 数组num中maxNum>target，直接返回false。

之后我们创建一个二维数组

vector<vector<int>dp(num.size(),vector<int>(target,0));

Dp[i][j] 

i表示 从数组num[0~i] 中选取任意个元素 j表示和，

如果相加存在等于j

则 dp[i][j]=1;

其中有两个边界

1.如果不选任何的正整数，则和可以为0：则dp[i][0]=1(0<i<num.size());

2.当i==0的时候只有num[0]可以选取 则dp[0][num[0]=1;

对于 i>0i>0 且 j>0j>0 的情况，如何确定 \textit{dp}[i][j]dp[i][j] 的值？需要分别考虑以下两种情况。

如果j>=num[i] 则当前数字num[i]可以选取，也可以不选取 只要一种情况为true 则都可以

如果j<num[i]，则无法选取

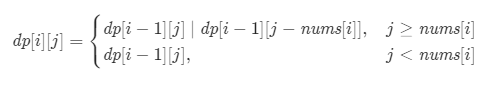
最终返回

dp[sum.size()-1][target]

为答案

   `class Solution
   {  
       bool canPartiton(vector<int>&nums)
       {
           sort(nums.begin(),nums.end());
           int total=0,len=nums.size();
           if(len<2||(len==2&&num[0]!=nums[1]))
               return false;  
           for(int i=0;i<len;i++)total+=nums[i];
           if(total%2!=0) return false;
           int half—total/2;
           if(nums[len-1]>half) return false;
           vector<vector<int>>dp(len,vector<int>(half+1,0));
           for(int i=1;i<len;i++) dp[i][0]=1;
           dp[0][nums[0]]=1;
           for(int i=1;i<len;i++)
           {
               for(int j=1;j<half+1;j++)
               {
                   if(j>=nums[i])
                       dp[i][j]=dp[i-1][j]||dp[i-1][j-nums[i]];
                   else
                       dp[i][j]=dp[i-1][j];
               }
           }
               return dp[len-1][half];
       }
   };