威伦特

解码生命

首页 文章 标签 关于

CNN

2022-11-25 12 min read # 深度学习

卷积神经网络（Convolutional Neural Networks, CNN）是一类包含卷积计算且具有深度结构的前馈神经网络（Feedforward Neural Networks），是深度学习（deep learning）的代表算法之一

LeNet-5是卷积神经网络的开山之作，也是一个较简单的卷积神经网络，出自论文：

《Gradient-based learning applied to document recognition》

这篇文章中，我们在LeNet-5的基础上，探索CNN是什么，了解它们是如何工作的，

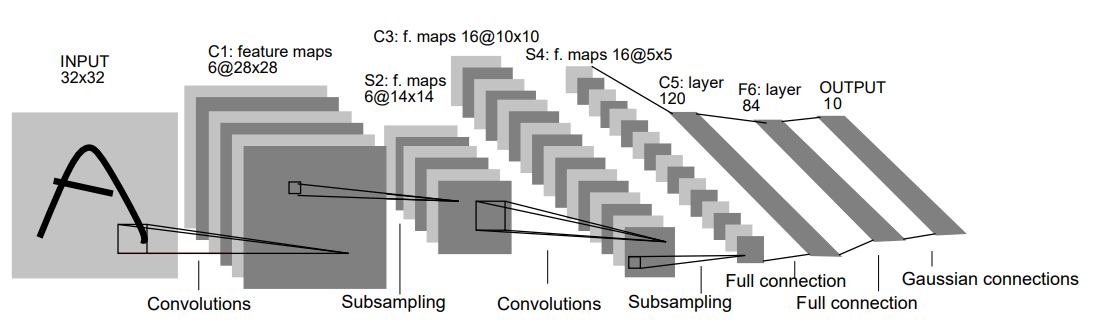
CNN是用来对图像分类的模型，CNN与普通的神经网络对比有如下优势：

优势1：能有效提取图像中关键的数值

用于计算机视觉问题的图像通常大小为 224x224 。如果构建一个神经网络来处理 224x224 彩色图像：包括图像中的 3 个颜色通道 （RGB），那么输入有 224 x 224 x 3 =150528个数值，如果神经网络中的隐藏层有 1024 个节点，因此我们必须训练 150528 x 1024 =仅第一层就有 150+ 百万个权重。

同时我们也知道，并不是图像中每一个值都需要作为输入，图像中像素是否有用关键在于其在图像中所处的环境。并不需要要查看图像中的每一个像素点。

优势2：能解决图像位置的偏移的问题

如果你训练了一个神经网络来检测狗，然而预测的图像可能和预测图像有所偏移。那么普通神经网络就不会激活相同的神经元。

而CNN能够准确的对图像进行预测，无论图像怎么偏移。

数据集

在这篇文章中，我们将通过MNIST手写数字数据集来进行图像的分类。

来自 MNIST 数据集的示例图像
MNIST 手写数字数据集的示例图

MNIST 数据集中的每个图像都是 28x28，MNIST将每个数字进行了居中排列。

卷积层

卷积层：就是将图像矩阵和卷积核卷积的数学运算。

下面是一个 3x3 卷积核示例：

img

通过将卷积核与输入图像卷积来生成输出图像矩阵。

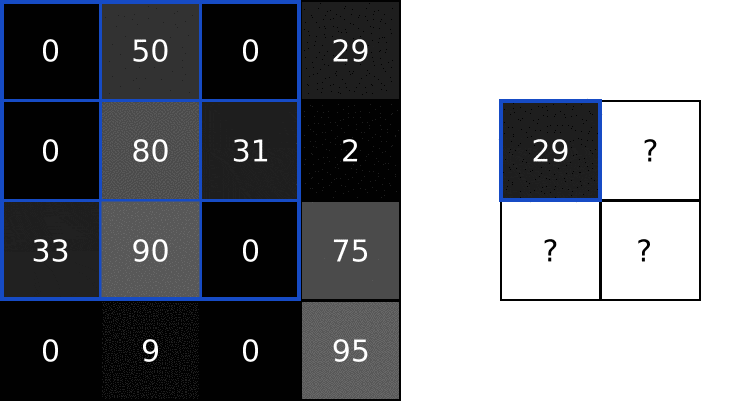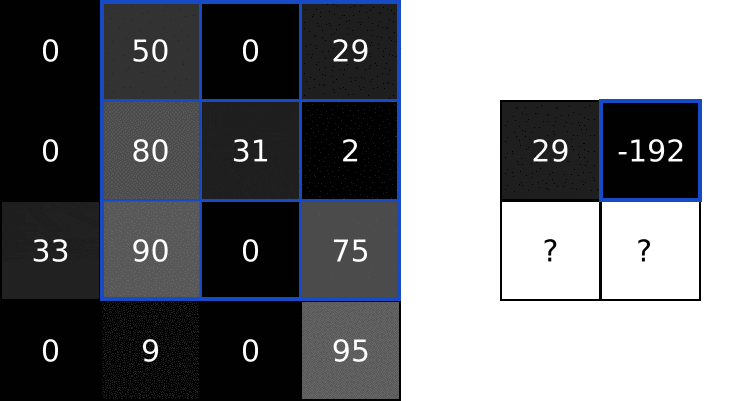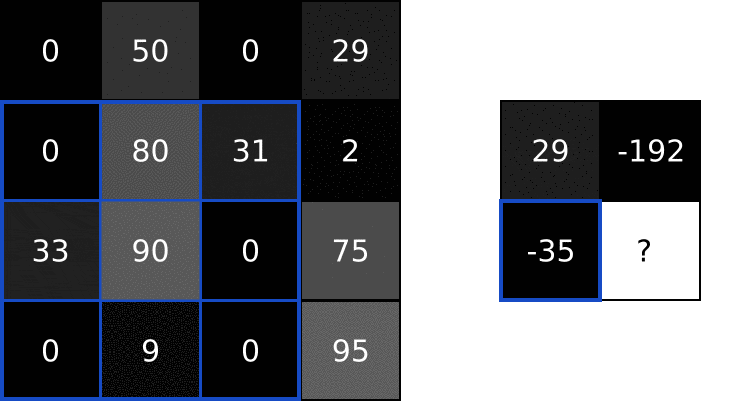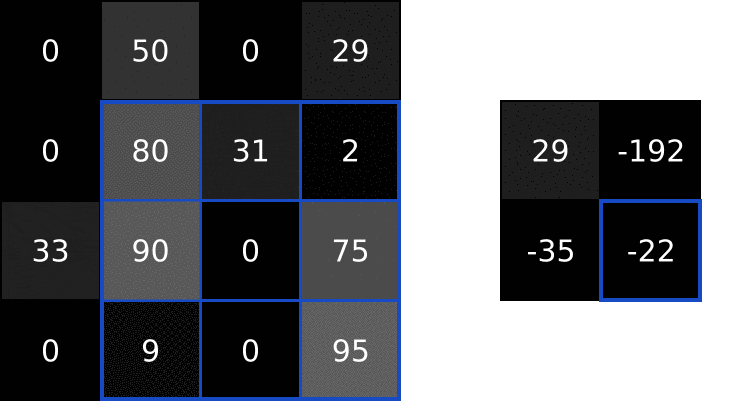
例子：将一个的4x4灰度图像和这个3x3卷积核进行卷积：

img

图像中的数字表示像素强度，其中 0 表示黑色，255 表示白色。我们将对输入图像和卷积核进行卷积，最后会生成一个 2x2 输出图像：

首先，让我们在图像的左上角叠加我们的卷积核：

img

接下来，我们在重叠的图像值和过滤器值之间执行逐元素乘法。以下是结果，从左上角开始，向右，然后向下：

图像值 过滤器值 结果
0 -1 0
50 0 0
0 1 0
0 -2 0
80 0 0
31 2 62
33 -1 -33
90 0 0
0 1 0

将所有的结果相加：

62−33=2962-33=29

最后，我们将结果放置在输出图像的目标像素中。由于我们的卷积核叠加在输入图像的左上角，因此我们的目标像素是输出图像的左上角像素：

img

做同样的操作，直到输出矩阵被填满：

img

使用卷积核卷积图像有什么作用？我们可以从我们一直在使用的示例 3x3 过滤器开始，它通常被称为垂直Sobel 卷积核：

img

还有水平Sobel卷积核：

img
  • 垂直 Sobel 卷积核能检测图像垂直边缘。
  • 水平 Sobel 卷积核能检测水平边缘。

也就是说：经过卷积核输出图像中的明亮像素（具有高值的像素）表示原始图像中存在很强的边缘。

Padding

很多时候，如果希望输出图像与输入图像的大小相同。那么可以在图像周围添加零，以便我们可以在更多位置覆盖卷积核。这样的操作就称为Padding。如下图，4x4图像通过padding一层，经过卷积层后，产生了相同大小的输出图像

img

padding 存在的意义在于

  • 为了不丢弃原图信息
  • 为了保持feature map 的大小与原图一致
  • 为了让更深层的layer的input依旧保持有足够大的信息量
  • 为了实现上述目的，且不做多余的事情，padding出来的pixel的值都是0，不存在噪音问题。

在LeNet-5论文中，作者将数字图像通过了一个带有 8 个卷积核的卷积层作为我们网络中的初始层。图像从 32x32 转换为了 28x28x8 的输出体积：

池化层

图像中的相邻像素往往具有相似的值，因此卷积层通常也会为输出中的相邻像素生成相似的值。因此，卷积层输出中包含的大部分信息都是多余的。

池化层解决了这个问题，池化层通过对卷积后的图像进行下采样，是缩小图像的尺寸(长、宽、通道数)，从而减少计算量、内存使用量、参数个数，从而达到一定的尺度、空间不变性，和降低过拟合可能性的目的。

池化层有最大池化，均值池化，全局平均池化，混合池化，随机池化等池话操作

下图示例了一个4x4的图像进行最大池化缩小为2x2的图像：

img

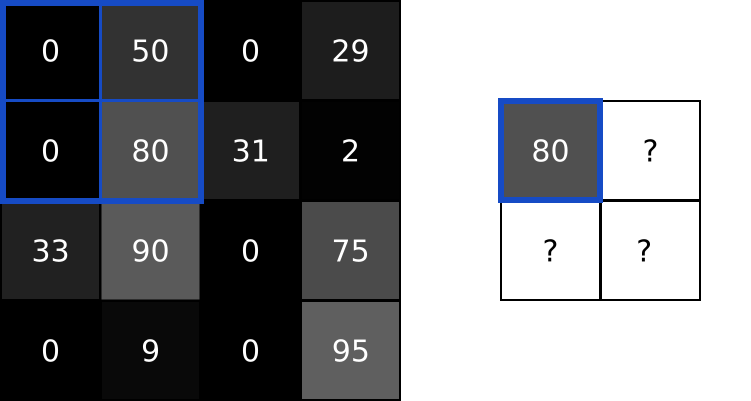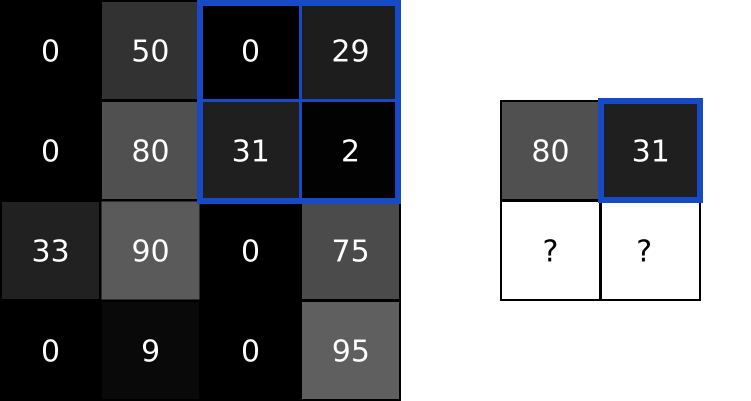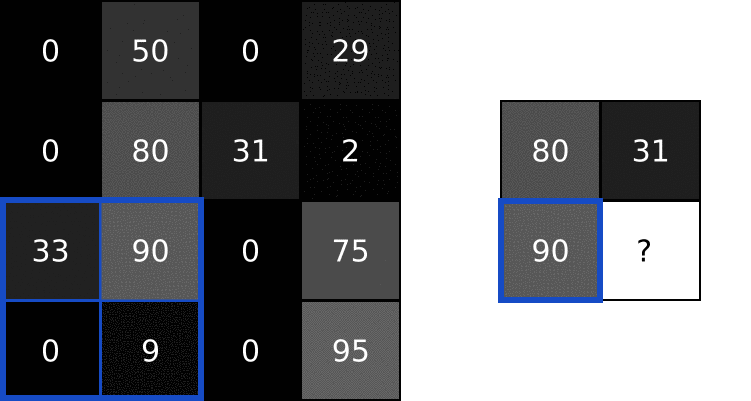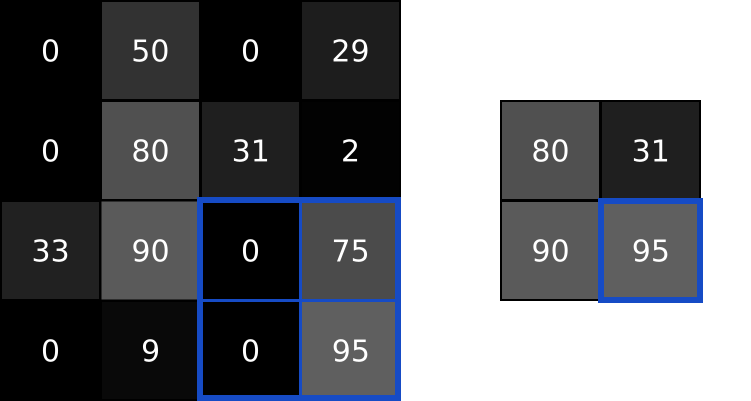
在LeNet-5论文中，作者将卷积后的图像通过池化层，让图像从 28x28x8转换为了 14x14x6 的输出体积：

全连接层

在图像经过了多层卷积层和池话层后，将其展开为一个n元向量，作为输入传入全连接层，经过softmax，概率最高的节点所代表的数字就是CNN预测的数字。

img

outs(c)=etc∑jetjout_s(c)=\frac{e^{t_c}}{\sum_je^{t_j}}

注意：LeNet-5 与现在通用的卷积神经网络在某些细节结构上还是有差异的， LeNet-5 采用的激活函数是 sigmoid，而目前图像一般用 tanh，relu，leakly relu 较多；多分类最后的输出层一般用 softmax，而 LeNet-5 采用的是欧式距离。

反向传播

损失函数

使用Softmax与交叉熵损失函数，作为损失函数。

L=−ln(P(c))\\L=-ln(P(c))

其中P(c)为当前实际数字的概率

求导过程

(1)∂L∂outs(i)={0,i≠c−1p(c),i=c\frac{∂L}{∂out_s(i)}=\begin{cases} 0,\quad i\neq c\\ -\frac{1}{p(c)}, \quad i=c \end{cases} \tag{1}

当 k≠c\ k \neq c时：

(2)∂outs(c)∂tk=∂outs(c)∂∑jetj∗∂∑jetj∂tk=−etcetk(∑jetj)2\frac{∂out_s(c)}{∂t_k}=\frac{∂out_s(c)}{∂\sum_je^{t_j}}*\frac{∂\sum_je^{t_j}}{∂t_k} \\=\frac{-e^{t_c}e^{t_k}}{({\sum_je^{t_j})^2}} \tag{2}

当 k=c\ k = c时：

(3)∂outs(c)∂tc=etc(∂∑jetj−etc)S2\frac{∂out_s(c)}{∂t_c}=\frac{e^{t_c}(∂\sum_je^{t_j}-e^{t_c})}{S^2} \tag 3

其中，S=∑ieti其中，S=\sum _{i}e^{t_i}

将②和③联合起来：

(4)∂outs(c)∂t={−etcetk(∑jetj)2，k≠cetc(∂∑jetj−etc)S2,k=c\frac{∂out_s(c)}{∂t}=\begin{cases} \frac{-e^{t_c}e^{t_k}}{({\sum_je^{t_j})^2}}，\quad k\neq c\\ \frac{e^{t_c}(∂\sum_je^{t_j}-e^{t_c})}{S^2}, \quad k=c \end{cases} \tag{4}

接下来使用链式法则得到权重对损失函数的导数：

t=w∗input+bt=w*input+b

(5)∂t∂w=input\frac{∂t}{∂w}=input \tag 5

(6)∂t∂b=1\frac{∂t}{∂b}=1 \tag 6

(7)∂t∂input=w\frac{∂t}{∂input}=w \tag 7

联立①④⑤：

∂L∂w=∂L∂out∗∂out∂t∗∂t∂w\frac{∂L}{∂w}=\frac{∂L}{∂out}*\frac{∂out}{∂t}*\frac{∂t}{∂w}

联立①④⑥：

∂L∂b=∂L∂out∗∂out∂t∗∂t∂b\frac{∂L}{∂b}=\frac{∂L}{∂out}*\frac{∂out}{∂t}*\frac{∂t}{∂b}

联立①④⑦：

(8)∂L∂input=∂L∂out∗∂out∂t∗∂t∂input\frac{∂L}{∂input}=\frac{∂L}{∂out}*\frac{∂out}{∂t}*\frac{∂t}{∂input} \tag 8

接下来对w，b，input进行梯度下降更新数值：

input=input−μ∂L∂inputw=w−μ∂L∂wb=b−μ∂L∂binput=input-\mu\frac{∂L}{∂input}\\ w= w-\mu\frac{∂L}{∂w}\\ b= b-\mu\frac{∂L}{∂b}\\

反向传播：池化层

在对全连接层的input进行更新后，继续向后传递到池化层：

当然，我们无法对池化层进行训练，我们所做的仅仅是将新梯度下降后的input数值，还原到经过卷积后的图像的原位置上,并将其他位置的值设置为0

img
将 2x2 图像向后传播到 4x4 图像示例

为什么其他位置要设置为0？因为在CNN模型的训练过程中，其他位置根本没有参与进来，也就是说其他位置的值根本不会改变输出。

反向传播：卷积层

在卷积层，我们需要优化卷积核的权重，在之前我们已经得到了卷积层输出对损失函数的导数 ∂L∂conv\ \frac{∂L}{∂conv}

所以我们只需要计算 ∂conv∂filters\ \frac{∂conv}{∂filters},也就是卷积核权重对卷积输出的导数

更改任何卷积核权重都会影响卷积后的整个输出图像，因为每个输出像素在卷积期间都会使用到每个卷积核权重

img img

上图所示了，当仅仅改变卷积核一个数值的时候，输出图像的变化

数学表达式如下：

conv(i,j)=convolve(image,filter)=∑x=0height∑y=0widthimage(i+x,j+y)∗filter(x,y)conv(i,j)=convolve(image,filter) \\=\sum_{x=0}^{height}\sum_{y=0}^{width}image(i+x,j+y)*filter(x,y)

于是:

(9)∂conv(i,j)∂filter(x,y)=image(i+x,j+y)\frac{∂conv(i,j)}{∂filter(x,y)}=image(i+x,j+y) \tag 9

联立⑧⑨得到卷积核权重对损失函数的导数

∂L∂filter(x,y)=∑i∑j∂L∂conv(i,j)∗∂conv(i,j)∂filter(x,y)\frac{∂L}{∂filter(x,y)}=\sum_i\sum_j\frac{∂L}{∂conv(i,j)}*\frac{∂conv(i,j)}{∂filter(x,y)}

接下来对卷积核权重进行梯度下降：

∑x=0height∑y=0widthfilter(x,y)=∑x=0height∑y=0width(filter(x,y)−μ∂L∂filter(x,y))\sum_{x=0}^{height}\sum_{y=0}^{width}filter(x,y)= \sum_{x=0}^{height}\sum_{y=0}^{width}(filter(x,y)-\mu\frac{∂L}{∂filter(x,y)})

到此，完成了对CNN的向后传播整个过程，通过设置迭代条件可以不断优化各个权重，提高CNN模型的预测准确率

实现

在Keras中对 MNIST CNN的示例：Simple MNIST convnet (keras.io)

在其训练15代后，准确率高达99%

参考文献

CNNs, Part 1: An Introduction to Convolutional Neural Networks - victorzhou.com

CNNs, Part 2: Training a Convolutional Neural Network - victorzhou.com

《Gradient-based learning applied to document recognition》

《这可能是神经网络 LeNet-5 最详细的解释了！》

属于 @威伦特 RSS